Contenus
ToggleProjet sur la programmation linéaire : The Truman Show
Ce projet requiert des notions de programmation linéaire et des algorithmes d’optimisation combinatoire, notamment le Branch & Bound.

“We’ve become bored with watching actors give us phony emotions. We are tired of pyrotechnics and special effects. While the world he inhabits is, in some respects, counterfeit, there’s nothing fake about Truman himself. No scripts, no cue cards. It isn’t always Shakespeare, but it’s genuine. It’s a life.”
Début du projet

La télé-réalité rapporte des milliards d’euros par an. Mais pour faire la différence, il faut oser toujours plus. En tant que jeune diplômé-e de la célèbre école de cinéma et de l’audiovisuel Herr Guerard’s Blinded Academy, vous devez percer dans le métier, et le plus rapidement possible.
C’est ainsi que vous viens l’idée de faire de The Truman Show une réalité. Les villes fantômes ne manquent pas, mais votre budget est limité et vous devez gratter l’argent là où vous le pouvez. Afin de ne pas perdre une goutte de votre télé-réalité, vous devez quadriller la ville de caméra. La construction de ces dernières varie énormément d’un point à l’autre. Mais fort heureusement, vous vous rappeler des cours de l’éminent professeur Guerard concernant les problèmes linéaires en nombre entier (ILP).
« Une couverture par sommets ou transversale d’un graphe G est un ensemble C de sommets tel que chaque arête de G = (V, E) est incidente à au moins un sommet de Cv ∈ S {\displaystyle v\in S} . »
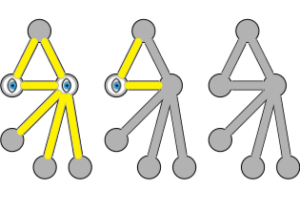
Concrètement celui revient à l’exemple suivant : Il y a 6 couloirs à contrôler et il faut placer le nombre minimal de caméras 360° de façon à ce que chaque couloir soit vu par au moins une caméra. Le nombre minimal est 2 et les deux caméras forment une couverture des sommets.
Le problème est écrit de façon suivante :
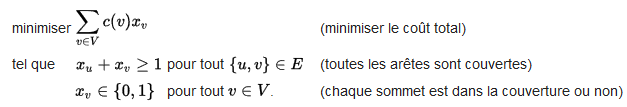
Avec c(v) le coût d’installation de la caméra au sommet v. xv vaut 1 si on construit une caméra sur le sommet v, sinon il vaut 0. Pour chaque arête (u,v), on pose la contrainte suivant xu+xv inférieur à 1.

Les intersections et angles droits sont des sommets, la route entre deux sommets est une arête. Un rond-point compte pour un seul sommet. Seul les routes sont des arêtes (pas les parkings, pas les voies à sens unique ni les routes non balisées). Le coût des caméras est égal au nombre de traits des lignes de démarcations des routes adjacentes (jusqu’aux prochains sommets).
Notation
- Fabriquer le graphe correspondant (2 points)
- Fabriquer l’ILP (3 points)
- Trouver une solution de base (5 points)
- Dérouler l’algorithme du Branch&Bound (10 points)
Vous avez le droit d’utiliser n’importe quel simplexe pour résoudre les PL.
