This project requires knowledge of linear programming and combinatorial optimization algorithms, including Branch & Bound.
“We've become bored with watching actors give us phony emotions. We are tired of pyrotechnics and special effects. While the world he inhabits is, in some respects, counterfeit, there's nothing fake about Truman himself. No scripts, no cue cards. It isn't always Shakespeare, but it's genuine. It's a life. ”
Beginning of the project
Reality TV brings in billions of euros a year. But to make a difference, you have to always dare more. As a recent graduate of the famous film and audiovisual school Herr Guerard's Blinded Academy, you need to break into the profession as quickly as possible.
This is how you got the idea to make The Truman Show a reality. There is no shortage of ghost towns, but your budget is limited and you have to scratch the cash where you can. In order not to lose a drop of your reality TV, you must crisscross the city with your camera. The construction of the latter varies enormously from one point to another. Fortunately, you will remember the lessons of the eminent Professor Guerard on linear integer problems (ILP).
" A peak coverage Where transverse of one graph G is a set VS of vertices such that each edge of G = (V, E) is incident at at least one vertex of VSv ∈ S {\ displaystyle v \ in S}. "
Concretely, this amounts to the following example: There are 6 lanes to control and the minimum number of 360 ° cameras must be placed so that each lane is seen by at least one camera. The minimum number is 2 and the two cameras form a coverage of the vertices.
The problem is written as follows:
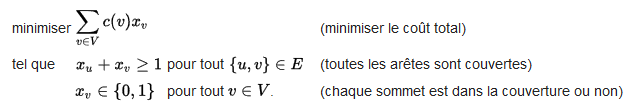
With c (v) the cost of installing the camera at the top v. xv is worth 1 if we build a camera on the top v, otherwise it is 0. For each edge (u, v), we set the following constraint xu+ xv less than 1.
Intersections and right angles are vertices, the road between two vertices is an edge. A roundabout counts as a single summit. Only roads are ridges (not parking lots, one-way lanes or unmarked roads). The cost of the cameras is equal to the number of lines of the demarcation lines of the adjacent roads (up to the next vertices).
Rating
- Build the corresponding graph (2 points)
- Making the ILP (3 points)
- Find a basic fix (5 points)
- Unroll the Branch & Bound algorithm (10 points)
You have the right to use any simplex to solve PLs.
EN 
FR 
ES