LP: large M method

Big M method

When the simplex has artificial variables, it is possible not to find an obvious starting solution (test if the origin is in the definition field). In this case, a starting solution must be found using the big M method.

This method computes an auxiliary problem before solving the simplex of the linear program, which is why it is called a two-phase simplex.

Why an artificial variable?

Before explaining how to obtain a solution to start the simplex, it is important to understand why it is necessary to add an artificial variable in addition to the slack variable.

Take as an example the following linear program:

Let's add the variance variables:

The simplex starts by taking the base variables at zero, so with the following vector (0, 0, -19, 32). This is impossible because X3 cannot take a negative value. This is why a new variable must be added, which will therefore be artificial.

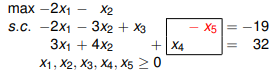
Here the vector (0, 0, 0, 19, 32) is a feasible solution. But since it is an artificial variable, it must be possible to remove it from the Simplex in order to be able to find a global solution. It is therefore necessary that X5 = 0. To check if this is possible, we are looking to minimize X5.

Construction of Phase 1

We prepare in a similar way to the initial table of the Simplex method, but with some differences. By taking the previous example, we try to solve the following problem:

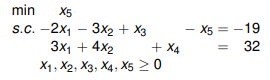
We know that only X4 and X5 are in the base, so the first step is to express the objective function with the non-base variables (here X1, X2, X3). In the example, this is possible thanks to the first constraint.

The first step is to solve the following linear program:

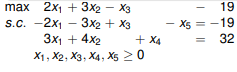
Phase 2

The second phase of the Two-Phase method is developed exactly like the Simplex method, except that before starting the iterations it is necessary to remove the columns corresponding to the artificial variables, and to reconstruct the original table.

• Delete the columns of artificial variables: If we have come to the conclusion that the initial problem has a solution, we need to prepare our table for the second phase. This step is very simple, you just have to delete the columns corresponding to the artificial variables.
• Reconstruction of the initial table: The initial array, in this case, remains roughly equal to the last array of the first phase. The line of the objective function should be modified only by that of the initial problem and recalculate the line Z (in the same way as in the first table of phase 1).

The stopping condition is the same as in the Simplex method. In other words, when in the indicator line none of the values of the reduced costs is negative (because we are in the case of a maximization).

The previous simplex gives for optimal solution Z = 0 with the vector (0, 19/3, 0, 20/3, 0). That means that it is possible to do without the artificial variable and that the solution found is in the space of definition of the initial problem (since X5 does not intervene and that it is out of base). The final solution gives the following simplex:

The last step of phase 1 consists of taking the initial objective function (here -2X1 - X2) and replacing all the base variables with non-base variables (here X2 and X4 are in the base, X1 and X3 are outside the bases ).

We have for the first constraint X2 = 19/3 - 2 / 3X1 + 1 / 3X3, we can therefore rewrite the objective function by: Z = - 4 / 3X1 - 1 / 3X2 -19/3.

From this point, all the iterations, until reaching the optimal solution of the problem, show no difference with the Simplex method.

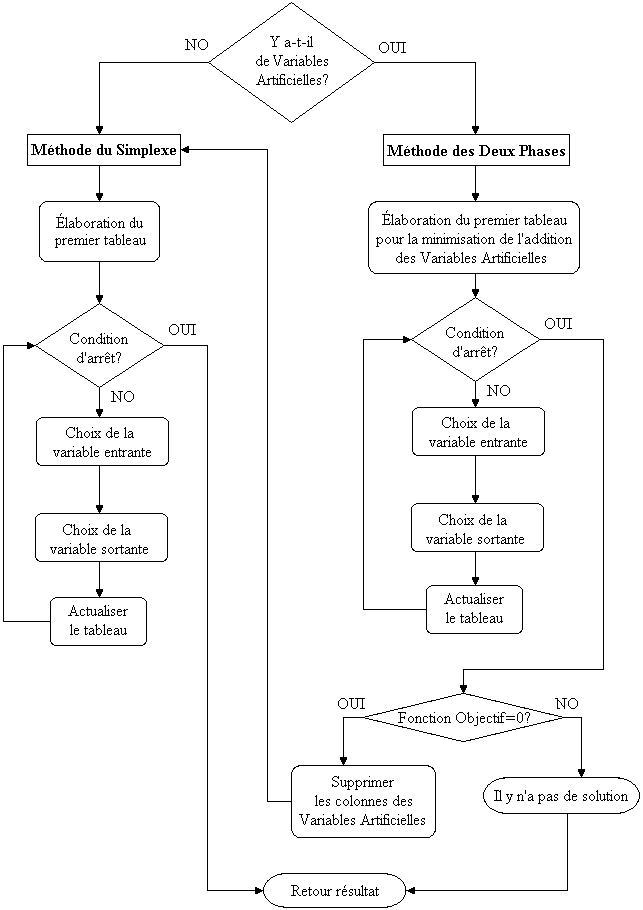
Simplex algorithm

Here is the revisited simplex algorithm: