Contents
ToggleAchievable domain
A solution of one linear problem is said to be feasible if all the constraints are satisfied. The feasible domain contains all the feasible solutions of the problem. The optimal solution is the “best” feasible solution(s).
To know if a solution is feasible, it suffices to test if all the constraints are satisfied, that can be done by hand or in matrix form.
By hand :
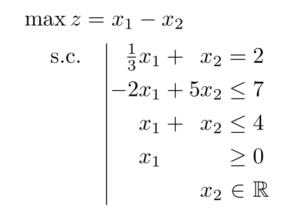
Let's check if the solution (3, 1) is feasible.
The first equation gives 3 * 1/3 + 1 = 2, the constraint is satisfied.
The second inequality gives -2 * 3 + 5 * 1 = -1 ≤ 7, the constraint is satisfied.
The third inequality gives 3 + 1 = 4 ≤ 4, the constraint is satisfied, we say that it is saturated.
Both type constraints are satisfied.
The solution is achievable. The value of the objective function is z = 3 - 1 = 2.
From a matrix point of view: we must multiply the matrix of the linear program by the solution vector and compare the result to the right members of the linear program
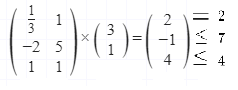
Achievable domain (or definition domain)
Each constraint can be likened to an equation dividing the plane in two. For example the equation ai* x1 + bi* x2 = ci divides the plane into two half-planes P1 and P2 equation:
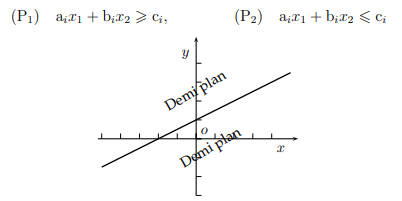
The less than or equal constraint will determine one half-plane, the greater or equal constraint will determine the other half-plane. To know in which half-plane are the feasible solutions for the constraints, it suffices to test a simple example and to determine if it is feasible or not.
For example for the constraint: x1 + x2 ≤ 4, the solution (0,0) is feasible, so the origin is in the feasible half-plane.
The intersection of all feasible half-planes constitutes the feasible domain. The latter can be bounded or unbounded.

