Contents
ToggleCorrected Exercises for Special Cases (Big M) in Linear Programming
This tutorial offers exercises corrected on particular cases (degeneration, large M, two-phase simplex).

Tutorial
A brooker needs, for its customers, 108 MWh of electricity for city 1 and 96 MWh of electricity for city 2. However, Kirchhoff's laws do not allow a distributor to target a single city for the energy transit. Two distributors serve these cities: Distributor A can send 12 MWh to city 1 and 8 MWh to city 2 per lot purchased; Distributor B can send 9 MWh to city 1 and 12 MWh to city 2 per lot purchased. The lots all have the same price. How many lots must the brooker buy to meet the energy demand of the two cities? Solve by graphical method and by the simplex.
The linear program is as follows: X1 for the first batch and X2 for the second batch
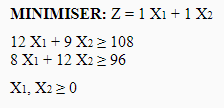
Which gives for graphic resolution:
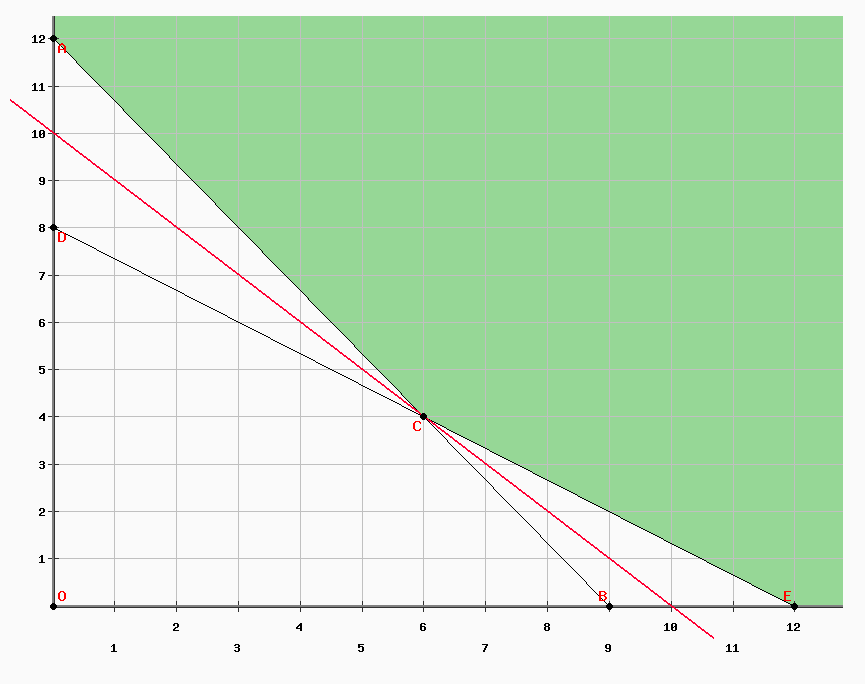
The gradient is (-1, -1) because it is a minimum (min f (x) = - max -f (x)). In the field of definition in green, point C is the only extremum being a global optimum. Solving the previous system in the form of equality gives the coordinates (6, 4) with Z = 10.
For the resolution of the simplex it is necessary above all to reduce to the standard form.

It is necessary to solve the simplex in two phases in order to eliminate the artificial variables:
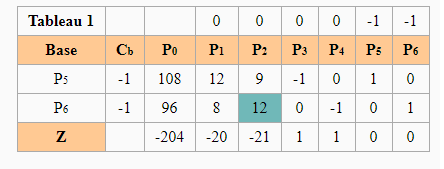
And the result of the first phase. We notice that Z = 0 so there is a solution to the problem:
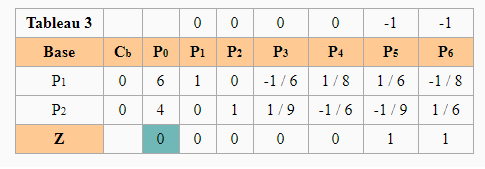
For the second phase, row Z is recalculated after removing the columns of artificial variables. To do this, we take the good coefficients of the objective function (-1, -1, 0, 0):
- (0) + (-1 * 6) + (-1 * 4) = -10 for column b (P0)
- (- 1) + (-1 * 1) + (-1 * 0) = 0 for column P1
- (- 1) + (-1 * 0) + (-1 * 1) = 0 for column P2
- (0) + (-1 * -1 / 6) + (-1 * 1/9) = 1/18 for column P3
- (0) + (-1 * 1/8) + (-1 * -1 / 6) = 1/24 for column P4
Which gives the following simplex:

All the coefficients except column b are positive therefore the simplex already has the optimal solution which is Z = 10 with the vector (6, 4, 0, 0).
Exercise 1
An electricity reseller promised his customers that at least 25% of his electricity would be of renewable origin. He calculated that for the coming year he will have a market of at most 18 TWh. He has also pre-selected three suppliers from whom he will buy his electricity wholesale. Here are the quantities (in TWh), the renewable electricity rate and the margin generated (in thousands of euros / TWh) that these three producers can provide. From which producers and in what quantity should this reseller buy his electricity to obtain the best possible profit? Solve the linear problem with the large M method using Excel.

After standard formatting, the problem is as follows, there are more constraints than variables, so we can solve the primal:

The problem is solved in two phases because there is an artificial variable. Here is the table of the first phase:

And the solution of the first phase, we notice that Z = 0 so there is a solution to the problem:

After recalculating the coefficients of Z, the second phase begins with the following table:

And ends with the following table:
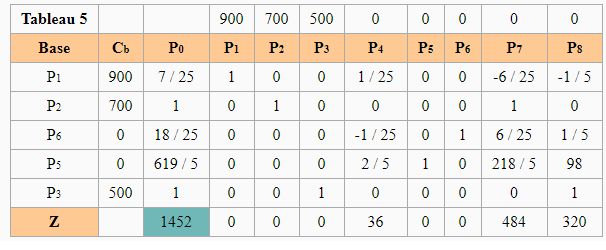
Exercise 2
Solve the following linear program (by Excel):
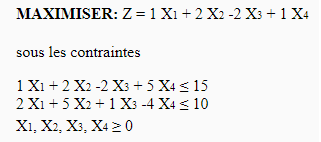
It is noticed above all that there are more variables than constraints, it is thus necessary to solve the linear program while passing by the simplex and the complementary variations. The dual in canonical then standard form is as follows:

We must therefore solve the problem of the large M in order to eliminate the artificial variables. The simplex to be solved is as follows:
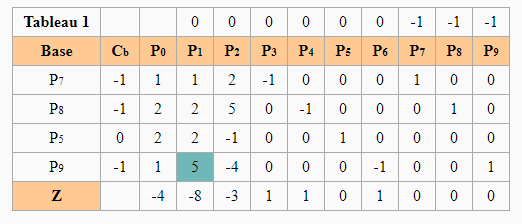
Which results in:

By eliminating the artificial variables and returning to the dual program we have the following table:
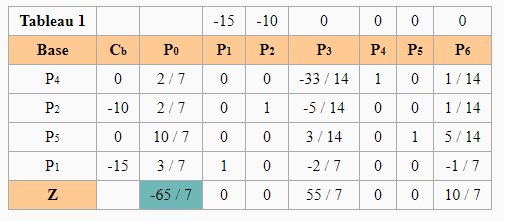
The optimal solution has for vector (3/7, 2/7) with Z = 65/7. Let's go through the complementary differences to find a solution to the primal.
The two variables are not zero, therefore the constraints of the primal are saturated. The constraint 2 and 3 of the dual are unsaturated, so the second and third variable of the primal are zero. The following problem must therefore be solved:
- X1 + 5 X4 = 15
- 2 X1 - 4 X4 = 10
The solution vector of the primal is (55/7, 0, 0, 10/7) and Z = 65/7. There is strong duality so it is an optimal solution of the primal.
Exercise 3
When an eco-district produces more energy than it consumes, then it sells the surplus energy to the neighborhood and to the network. The eco-district therefore seeks to maximize its earnings based on offers from the local market. The market offers are as follows:
| Offer n ° | 1 | 2 | 3 | 4 | 5 | 6 |
| Profit | 10 | 8 | 15 | 4 | 1 | 5 |
| Energy (in kWh) | 5 | 10 | 10 | 5 | 1 | 7 |
The problem is formulated as follows: the eco-district seeks to gain the maximum profit for a sale of energy of 25 kWh. The eco-district must sell all of the energy surplus.
To solve this problem, consider that each offer is represented by a variable (in percentage of acceptance of the offer) which will be between 0 and 1.
The problem is formulated as follows:

Which gives as standard form:
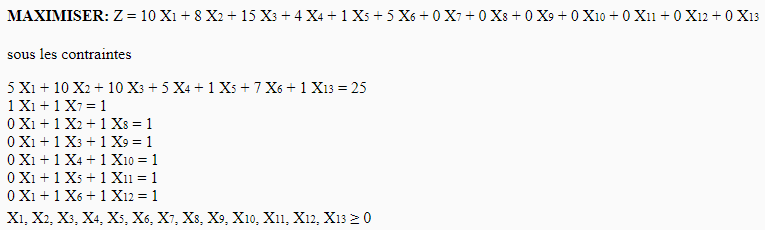
Let's start by solving the big M:

After solving the large M and returning to the standard form:

We notice that the value Z for the variable 1, 2, 3, 4, 5 are at zero so there is an infinite number of solutions. The solution obtained here is Z = 166/5 with the vector (1, 9/10, 1, 0, 1, 0).
