Contenus
ToggleExercices corrigés sur les problèmes de flot maximum
Cette page contient divers exercices corrigés sur les problèmes de flot max. Ces problèmes utilisent principalement l’algorithme Ford-Fulkerson et la solution min-cut.

Exercice 1
A l’aide de la méthode de Ford-Fulkerson, calculez un débit maximal dans le réseau suivant :

Exercice 2
La figure ci-dessous montre un réseau de flux sur lequel un flux s-t est affiché. La capacité de chaque bord apparaît sous la forme d’une étiquette à côté du bord, et les nombres dans les cases indiquent la quantité de flux envoyée sur chaque bord. (Les arêtes sans numéros encadrés n’ont pas de flux envoyé sur elles.) Quelle est la valeur de ce flux ? Est-ce un débit s-t maximum dans ce graphique ? Sinon, trouvez un débit s-t maximum. Trouvez une coupe minimale. (Spécifiez quels sommets appartiennent aux ensembles de la coupe.)

La valeur de ce débit est 17. Non, ce n’est pas un débit maximal. On peut trouver un débit maximum en regardant le réseau résiduel. Dans ce cas, à partir du flux donné, nous pouvons obtenir un flux maximum avec un seul chemin d’augmentation, s-z-y-x-w-t. Le débit maximum a donc la valeur 19.
On peut trouver une coupe minimale en utilisant le réseau résiduel pour le débit maximal final. À partir de s, trouvez tous les sommets accessibles à partir de s dans le réseau résiduel. Cela forme un ensemble dans la coupe minimale. Les autres sommets forment l’autre partie définie de la coupe. Ainsi, une coupe minimale dans ce cas sont les deux ensembles {s ; z} et {x ; w; y; t}.
Vous pouvez vérifier que la capacité de cette coupe (c’est-à-dire la capacité totale des arêtes de {s; z} à {x;w; y; t}, constituée des arêtes dirigées (s;w); (s; x) ; (z ; y) ; et (z ; t) vaut 19, comme le garantit le théorème flot max/coupe min.
Exercice 3
Décrivez un algorithme efficace qui trouve un nouveau flux maximum si la capacité d’un bord particulier augmente d’une unité. Décrivez un algorithme efficace qui trouve un nouveau flux maximum si la capacité d’un bord particulier diminue d’une unité.
Supposons que le bord de u à v augmente sa capacité de un. A partir du flux maximum précédent F, il suffit de faire une nouvelle itération de l’algorithme de Ford-Fulkerson avec le graphe modifié : Le graphe de flux résiduel augmente la capacité de l’arête (u; v) de un. Effectuez une recherche graphique pour voir s’il existe un chemin dans le graphique de flux résiduel le long duquel le flux peut augmenter. S’il y en a un, il doit y avoir un flux de taille un (car tous les flux sont des entiers). S’il n’y a pas de débit dans le graphique de débit résiduel, F est toujours le débit maximum.
Supposons que le bord de u à v diminue sa capacité de un. Si le débit maximal précédent F n’utilisait pas la pleine capacité de (u; v), un tel changement ne compte pas du tout. Sinon, nous mettons à jour le flux comme suit :
Étant donné que le flux entrant dans u est supérieur d’une unité au flux qui en sort et que le flux entrant dans v est inférieur d’une unité au flux qui en sort, il est impossible de transférer un flux unitaire de u vers v. Ainsi, recherchez dans le résidu graphe de flux pour un chemin de u à v le long duquel le flux peut augmenter de un. S’il existe un tel chemin, nous mettons à jour F avec le flux.
S’il n’y a pas un tel chemin, nous devons réduire le flux de s à u et de v à t d’une unité. Pour ce faire, nous trouvons un chemin de u à s dans le graphe de flux résiduel le long duquel le flux peut augmenter de un et un chemin de t à v le long duquel le flux peut augmenter de un. (Il doit y avoir de tels chemins, car nous avions un flux de s à t via (u; v).) Ensuite, mettez à jour F avec ces deux flux.
Exercice 4
Considérant le flux suivant, comment augmenter le flux ?

La coupe minimale est effectuée, nous connaissons donc les goulots d’étranglement sur le graphique. La somme des capacités à la source est de 22, et 24 au puits, on en déduit qu’on ne peut pas avoir plus de 22. Il faut donc trouver un chemin de à pour augmenter le débit de 2, et un chemin de à pour augmenter le flux par 1. L’exercice précédent donne à un algorithme une idée pour atteindre cet objectif. Nous pouvons augmenter les capacités sur des arêtes de coupe minimales.
Exercice 5
Dans le graphe biparti ci-contre, les sommets T1 … T6 représentent les travailleurs et les sommets E1 … E6 représentent les emplois. Un avantage relie un travailleur à un emploi si le travailleur possède les qualifications nécessaires pour occuper cet emploi. Comment allouer les emplois aux travailleurs pour minimiser le nombre de chômeurs ?
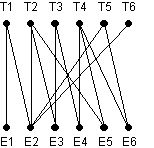
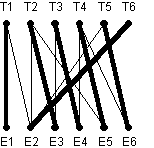
Attribuer un travail à une personne équivaut à « sélectionner » un bord. Ti sont connectés à une source fictive d’une capacité de 1 (idem pour le Ei à un puits fictif). Les arêtes du graphe biparti ont une capacité de 1. Il recherche alors un flux maximum.
Exercice 6
Supposons que vous organisiez une conférence où des chercheurs présentent des articles qu’ils ont rédigés. Les chercheurs qui souhaitent présenter un article envoient une communication aux organisateurs de la conférence. Les organisateurs de la conférence ont accès à un comité de relecteurs qui sont chacun disposés à lire des articles chacun.
Chaque soumission d’article est examinée par un maximum de réviseurs. De plus, chaque soumission a un sujet particulier et chaque examinateur a une spécialisation pour un ensemble de sujets, de sorte que les articles sur un sujet donné ne sont examinés que par les examinateurs qui sont des experts sur ce sujet.
Les organisateurs de la conférence doivent décider quels examinateurs examineront chaque article (ou, de manière équivalente, quels articles seront examinés par quels examinateurs). Expliquez comment ils pourraient utiliser un réseau de flux pour résoudre ce problème.
Il existe un ensemble A d’articles et un ensemble B de relecteurs. Ajoutez une arête dirigée (α,β) au graphe si un article α dans A peut être révisé par un relecteur β dans B, à savoir que l’article porte sur un sujet dans lequel le relecteur est un expert. Définissez la capacité de cette arête sur be 1. Ajouter un sommet s (source) et un sommet t (terminal). Pour chaque α dans A, ajouter une arête (s, α) de capacité mA. Pour chaque β de B, ajouter une arête (β , t) de capacité mB. Exécutez Ford-Fulkerson pour obtenir le débit maximum et calculez la coupe correspondante (A,B). Cela donne l’ensemble des arêtes qui correspondent à l’attribution des articles aux relecteurs.
Exercice 7
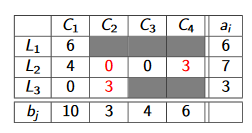
Soit un ensemble de machines et de tâches. Une machine Li peut être utilisée au maximum ai time. Une tâche Cj peut être utilisée au plus bj temps. Le tableau de l’offre et de la demande représente les machines et les tâches, ainsi que la capacité à effectuer une tâche sur une machine donnée (vide).

Créez un graphe biparti, puis faites une source fictive (puits fictif) avec des capacités d’arc ai (et bj). Ensuite, résolvez le problème de flux.