Contenus
ToggleExercices corrigés sur les bases de la théorie des graphes (modélisation en graphe et arbres)
Cette page montre quelques exercices corrigés sur la modélisation en graphe et arbres. Le but de ces exercices est d’apprendre à modéliser un problème grâce aux concepts et bases de la théorie des graphes. La majorité des problèmes présentés sont des simplexes aussi solvable avec la méthode classique.

Exercice 1
Deux joueurs ont 2 lots d’allumettes ou plus. A chaque tour, le joueur suivant peut retirer un certain nombre d’allumettes d’un lot (selon la règle choisie). Le joueur qui supprime la dernière allumette perd.
Modélisez ce jeu avec un graphe dans le cas où l’on dispose de deux piles contenant chacune trois allumettes, et où un joueur peut retirer une ou deux allumettes chacune.
Quel coup le premier joueur doit jouer pour gagner la partie ?

Le graphe est à lire de gauche à droite. Un joueur commence sur le noeud 3,3 et chaque coup fait prendre le trajet d’une arête vers un autre noeud. Le joueur atteignant 0,0 à perdu.
Si le joueur 1 joue, il a gagné si l’ensemble des chemin vers 0,0 est de taille impaire, ce qui n’est jamais le cas, il n’y a pas de stratégie automatiquement gagnante.
Exercice 2
Le graphique suivant montre les couloirs d’un musée. Un garde placé dans un couloir peut surveiller deux jonctions placées à ses extrémités. Combien de gardes sont nécessaires (et comment les placer) pour que toutes les intersections sont surveillées ?
Si nous plaçons maintenant des gardes aux intersections, en supposant qu’un garde peut surveiller tous les couloirs menant à ce carrefour, combien de gardes sont nécessaires ?

Chaque garde sera placé sur une arête et pourra surveiller deux intersections (sommets). Le graphe a 11 sommets ; il faudra au moins six gardes. Il faut donc trouver un ensemble (minimum) d’au moins six arêtes, tel que chaque sommet soit incident à au moins une de ces arêtes. Le graphique ci-dessous fournit une solution (arêtes plus épaisses).
Cette fois, les gardes sont aux sommets et surveillent les arêtes. Il doit y avoir un ensemble de sommets tel que chaque arête soit incidente à au moins un de ces sommets. Le graphique ci-dessous fournit une solution utilisant 6 sommets (sommets blancs).

Exercice 3
Skynet est un réseau à 15 sommets. Vous pouvez aller de chaque sommet à au moins sept autres sommets par lien. Peut-on passer par lien d’un sommet X à chacun des autres ?
Soit A un sommet quelconque. X est lié à au moins 7 villes différentes. Nous avons donc un réseau de 8 sommets reliés par des liens. Dans un sommet, vous pouvez également vous connecter à au moins sept autres sommets ; il y a donc un nouveau réseau de 8 sommets. Il doit y avoir un sommet partagé dans ces réseaux, car sinon le réseau aurait au moins 16 sommets. X est relié à A en au plus deux plans, par ce sommet commun ; il est relié à toutes les autres villes.
Exercice 4
Un réseau est composé de sept usines. Une ville est liée à exactement deux usines. Deux usines partagent exactement une ville. Combien de villes sont desservies par le réseau ?
Les usines sont les sommets et les villes sont représentées par une arête reliant deux sommets. La règle 2 implique qu’il n’y a pas d’arêtes multiples et que tout couple de sommets est adjacent ; c’est-à-dire que le graphe est complet ; c’est K7, graphe complet de 7 sommets, soit 21 liens.
Exercice 5
Considérons le programme linéaire suivant :

Où X est 0 ou 1. Déterminer, avec un problème de graphe, une solution qui maximise la fonction objectif (somme des X).
Un sommet représente une variable. Deux sommets sont connectés s’ils sont dans la même inégalité. Le problème est de trouver un ensemble maximum de sommets où aucun couple de sommets n’a de lien direct.

Exercice 6
Considérant un jeu de dominos utilisant les nombres 0, 1, 2, 3, 4, comme sur chaque domino comprend deux chiffres distincts, comme 1 et 3, le problème suivant est proposé : est-il possible d’aligner tous les dominos de sorte que lorsque deux pions « toucher » les numéros « au contact » sont identiques ?
Montrer le problème sous la forme d’un graphe complet K5. Le problème est de trouver un cycle eulérien dans le graphe.

Exercice 7
Dans un groupe de personne, il y a toujours deux individus qui connaissent exactement le même nombre de membres du groupe. Démontrez cela.
On doit prouver que dans un graphe simple (sans arête double, sans boucle), il y a toujours deux sommets qui ont le même degré. On va raisonner par l’absurde et supposer qu’il y a un graphe simple à n sommets dont tous les degrés sont différents. Alors les degrés des sommets sont compris entre 0 et n−1, et donc si tous les degrés sont différents, comme on a n sommets et simplement n possibilités pour les degrés, toutes ces possibilités doivent être prises.
En particulier, il doit y avoir un sommet de degré 0 et un sommet de degré n−1. Mais c’est impossible, car ce dernier sommet devrait avoir une arête vers tous les autres, et ce n’est pas possible puisqu’un sommet est de degré 0, donc isolé.
Exercice 8
Soit G un graphe non-orienté simple d’ordre 2p (nombre d’arêtes). On suppose que le degré de chaque sommet est au moins égal à p. Démontrer que ce graphe est connexe.
Supposons par l’absurde que ce graphe ne soit pas connexe, et soient x, y deux sommets tels qu’il n’existe pas de chemin liant x à y. Alors, x a au moins p voisins, et il en est de même pour y. Mais les voisins de x sont forcément tous distincts des voisins de y : sinon, il existerait une chaine de longueur 2 joignant x à y.
Le graphe comprend donc au moins 1+1+p+p=2p+2 sommets (x, y, les voisins de x, les voisins de y). On obtient donc une contradiction puisque le graphe est d’ordre 2p.
Exercice 9
Une chèvre, un chou et un loup se trouvent sur la rive d’un fleuve ; un passeur souhaite les transporter sur l’autre rive mais, sa barque étant trop petite, il ne peut transporter qu’un seul d’entre eux à la fois. Comment doit-il procéder afin de ne jamais laisser ensemble et sans surveillance le loup et la chèvre, ainsi que la chèvre et le chou ?
Cette situation peut être modélisée à l’aide d’un graphe. Désignons par P le passeur, par C la chèvre, par X le chou et par L le loup. Les sommets du graphe sont des couples précisant qui est sur la rive initiale, qui est sur l’autre rive.
Ainsi, le couple (PCX,L) signifie que le passeur est sur la rive initiale avec la chèvre et le chou (qui sont donc sous surveillance), alors que le loup est sur l’autre rive. Une arête relie deux sommets lorsque le passeur peut passer d’une situation à l’autre.
En transportant la chèvre, le passeur passe par exemple du sommet (PCX,L) au sommet (X,PCL). Le graphe ainsi obtenu est biparti : les sommets pour lesquels le passeur est sur la rive initiale ne sont reliés qu’aux sommets pour lesquels le passeur est sur l’autre rive.
Naturellement, on ne considèrera pas les sommets dont l’une des composantes est CX ou LC car ces situations sont interdites. Il suffit ensuite de trouver un chemin (le plus court par exemple) entre la situation initiale (PCXL,-) et la situation finale souhaitée (-,PCXL). La figure suivante donne un tel chemin :
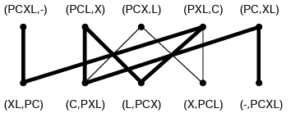
Exercice 10
Dans le graphe biparti suivant, les sommets T1, …, T6 représentent des travailleurs et les sommets E1, …, E6 des emplois. Une arête relie un travailleur à un emploi si le travailleur a les qualifications nécessaires pour occuper cet emploi. Comment affecter les emplois aux travailleurs afin de minimiser le nombre de sans-emploi ?
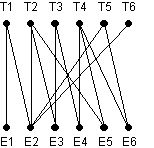
Affecter un emploi à une personne revient à « sélectionner » une arête. Chaque personne ne pouvant occuper qu’un seul emploi, et un emploi ne pouvant être occupé que par une seule personne, il faut donc sélectionner un nombre maximal d’arêtes de façon telle que ces arêtes n’ont aucun sommet commun (un tel ensemble est qualifié de stable maximal).
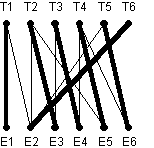
Exercice 11
Chaque jour, un groupe de 12 enfants fait une promenade, par rang de deux. Combien de jours peuvent-ils se promener si l’on souhaite qu’un enfant n’ait jamais deux fois le même voisin ? Et si maintenant la promenade se fait par rang de trois ?
Considérons le graphe complet K12 à 12 sommets, chaque sommet représentant un enfant. Le nombre d’arêtes de ce graphe est 12 x 11 / 2 = 66. Une promenade correspond à un ensemble de 6 arêtes non incidentes (n’ayant pas de sommet en commun) : chaque arête représente un rang (deux enfants) et chaque enfant ne peut appartenir qu’à un seul rang lors d’une promenade.
Il faut donc trouver le plus grand nombre d’ensemble (11 = 66/6) respectant cette règle :
1-2, 3-12, 4-11, 5-10, 6-9, 7-8 ; 2-3, 12-4, 11-5, 10-6, 9-7, 8-1 ; 1-3, 4-2, 5-12, 6-11, 7-10, 8-9 ; 3-4, 2-5, 12-6, 11-7, 10-8, 9-1 ; 1-4, 5-3, 6-2, 7-12, 8-11, 9-10 ; 4-5, 3-6, 2-7, 12-8, 11-9, 10-1 ; 1-5, 6-4, 7-3, 8-2, 9-12, 10-11 ; 5-6, 4-7, 3-8, 2-9, 12-10, 11-1 ; 1-6, 7-5, 8-4, 9-3, 10-2, 11-12 ; 6-7, 5-8, 4-9, 3-10, 2-11, 12-1 ; 1-7, 2-12, 3-11, 4-10, 5-9, 6-8
Exercice 12
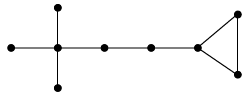
On s’intéresse aux graphes dont tous les sommets sont de degré trois. Construisez de tels graphes ayant 4 sommets, 5 sommets, 6 sommets, 7 sommets. Qu’en déduisez-vous ?
Les graphes dont tous les sommets sont de degré trois sont appelés graphes 3-reguliers ou graphes cubiques. La figure ci-dessous montre deux graphes cubiques, ayant respectivement 4 et 6 sommets. En effet, on constate aisément qu’il n’existe pas de graphes cubiques ayant un nombre impair de sommets : le nombre d’arêtes d’un graphe cubique à n sommets est 3n/2 qui n’est entier que lorsque n est pair.

Exercice 13
Un serveur peut acheminer un maximum de packages en même temps. Sept sous-stations sont reliées à un serveur, une sous-station ne peut pas envoyer de colis si certaines sous-stations utilisent déjà le lien. Le tableau suivant présente chaque sous-station de la capacité à envoyer un colis en fonction des autres. Par exemple, un colis de A ne peut pas être envoyé s’il existe déjà un colis de D mais peut être envoyé lorsque B a envoyé un colis.
Sous-station | A | B | C | D | E | F | G |
N’est pas avec | D,E | D,E,F,G | E,G | A,B,E | A,B,C,D,F,G | B,E,G | B,C,E,F |
Représenter les liens dans un graphique. Combien de paquets le serveur doit-il gérer en même temps (valeur maximale) ?
Nous représentons chaque sous-station par un sommet et deux sommets sont liés s’ils ne doivent pas être ensemble. Ainsi après une coloration de graphe, deux sommets de même couleur peuvent être ensemble.

Le graphe est 4-chromatique.
Exercice 14
Une école doit faire passer des épreuves écrites à quatre élèves : Pierre, Jean, Guillermo et Ibrahim. Sept disciplines sont concernées : mathématiques, physique, biologie, français, anglais, espagnol et histoire.
Pierre doit passer les mathématiques, la physique et l’anglais, Jean les mathématiques, la biologie et le français, Guillermo les mathématiques, l’anglais et l’espagnol et Ibrahim la physique, le français et l’histoire.
Quel est le nombre minimum de créneaux horaires à prévoir pour qu’aucun étudiant ne doive passer deux épreuves simultanément ? Quel est le nombre chromatique d’un graphe complet ? Comment borner les nombres chromatiques dans un graphe ?
Un sommet représente une discipline, une arête relie deux disciplines si elles ne peuvent avoir lieu en même temps. Le problème peut être résolu en recherchant un nombre minimum de couleurs. Le plus grand sous-graphe complet est K3, il y a donc au moins 3 couleurs. Le degré maximum est de cinq, il y a donc au plus 5 couleurs. Par expérimentation, le graphe est 3-chromatique.

Exercice 15
Le schéma suivant représente un carrefour.

Chaque branche à son propre feu tricolore avec indication fléchée de la direction autorisé, et voici les franchissements possibles de ce carrefour.

Les voitures ayant un feu vert ne doivent pas se croiser, ainsi A-C et B-E ne peuvent pas être autorisés simultanément.
Proposez une solution permettant d’alterné l’autorisation des feux dans ce carrefour.
Le graphe modélisant le carrefour est représenté ci-dessous. Son nombre chromatique est égal à 4 (il est 4-coloriable et contient un K4 regroupant les sommets AC, BD, CD et DA). Un ensemble de sommets de même couleur, par exemple ED, AC, AE et CA regroupe un ensemble de trajets pouvant s’effectuer en même temps (aucune incompatibilité).
Le nombre chromatique correspond alors au nombre minimum de « cycles » que doivent respecter les feux de signalisation de ce carrefour.
Pour notre exemple, nous aurons : 1. ED, AC, AE et CA 2. BA, BE, BD et EC 3. DC et DA 4. CD. D’autres solutions (4-colorations) sont naturellement possibles.

Exercice 16
Soit un graphe non orienté avec des sommets. Démontrer que toutes les propriétés suivantes sont équivalentes :
- est un arbre
- est connecté et si nous supprimons une arête, le graphe n’est plus connecté
- est connecté avec n-1 arêtes
- n’a pas de cycle jusqu’à ce que nous ajoutions une arête
- n’a pas de cycle avec n-1 arête
- un seul chemin entre n’importe quel couple de sommets
Pas de solution puisque cela est dans le cours sur les arbres !
Exercice 17
Nous voulons ajouter une batterie dans un réseau. Le graphique suivant montre le coût d’envoi d’énergie entre deux sous-stations du réseau et la quantité d’énergie envoyée par une sous-station. Vous devez placer la batterie dans une sous-station tout en minimisant le coût total.

Calculez la somme de tous les coûts à chaque sous-station, c’est-à-dire le coût de chaque chemin entre n’importe quelle sous-station et la sous-station choisie (arête * sommet).

Exercice 18
Nous allons voir un principe très important dans la théorie des graphes (lié aux enjeux sociaux) qui est la centralité (il existe beaucoup de calcul de centralité).
Un robot se promène sur le graphe ci-dessous. Partant d’un sommet quelconque s, appelé sommet de stockage, il doit déposer un cube sur chacun des autres sommets. Il possède suffisamment de cubes sur le sommet de stockage, mais ne peut transporter qu’un cube à la fois (il doit donc repasser par le sommet de stockage avant de livrer un autre cube).
Calculer, pour chacun des sommets du graphe, le trajet minimum que doit parcourir le robot si ce sommet est sommet de stockage. Quel est le « meilleur » sommet de stockage ?
Pour un sommet donné, il est nécessaire de calculer la somme des longueurs des plus courts chemins de ce sommet aux autres sommets (facile puisque nous avons à faire presque à un arbre). La figure suivante donne cette valeur pour le sommet A, puis pour tous les sommets du graphe. Le meilleur sommet de stockage est donc le sommet X.

Exercice 19
La mise en exploitation d’un nouveau gisement minier demande la réalisation d’un certain nombre de tâches. Le tableau suivant représente ces différentes tâches avec leurs relations d’antériorité.

Un sommet d’un graphe d’ordonnancement contient 3 éléments :
- Le nom de la tâche, le temps de réalisation au plus tôt et le temps de réalisation au plus tard.
- Un arc montre la dépendance d’une tâche à une autre avec une pondération du nombre de jour de la tâche antérieure. Ainsi A et B sont liés avec un poids de 120.
(au lieu d’un arc il est aussi possible de faire un graphe hiérarchique, i.e. le sommet le plus haut est la racine, ses successeur direct sont sur la hauteur suivante).
Un sommet fin est relié aux tâches sans successeur.
Le temps de réalisation au plus tôt est le plus long chemin d’une tâche à une autre dans le sens de la hiérarchie.
Le temps de réalisation au plus tard est le chemin le plus court dans le sens inverse de la hiérarchie.
Le chemin critique est le trajet de la première tâche à la fin dont le temps au plus tôt et au plus tard coïncident.
Construire le graphe d’ordonnancement.
En utilisant la méthode MPM, nous obtenons le graphe ci-dessous. Les dates au plus tôt et au plus tard sont calculées « par niveaux. Les tâches critiques, et le chemin critique sont indiqués en gras. Le temps minimum de réalisation de l’ensemble est lisible sur le sommet FIN : 1170 jours.

Exercice 20
Un groupe de 9 élèves se réunit chaque jour autour d’une table ronde. Combien de jours peuvent-ils se réunir si l’on souhaite que personne n’ait deux fois le même voisin ?
Désignons par 1,2,…,9 les 9 personnes et considérons le graphe complet K9 à 9 sommets. Une composition de la table correspond à un cycle hamiltonien de K9 (un cycle passant une et une seule fois par chaque sommet).
Si deux compositions de table correspondent à deux cycles ayant une arête commune, cela signifie que les deux personnes reliées par cette arête se retrouvent côte à côte. Ainsi, le problème revient à déterminer le nombre de cycles hamiltoniens disjoints de K9.
Le graphe K9 possédant 9 x 8 / 2 = 36 arêtes et chaque cycle utilisant 9 arêtes, ce nombre est au maximum égal à 4… Il vaut effectivement 4, comme le prouvent les 4 cycles hamiltoniens disjoints suivants :
1,2,3,9,4,8,5,7,6 — 1,3,4,2,5,9,6,8,7 — 1,4,5,3,6,1,7,9,8 — 1,5,6,4,7,2,8,1,9
Exercice 21
Cette fois, ces réunions quotidiennes concernent un groupe de 12 élèves, 6 filles et 6 garçons. On souhaite toujours que personne n’ait deux fois le même voisin, mais, cette fois, on souhaite également que chaque fille soit entourée de deux garçons. Combien de jours peuvent-ils se réunir ?
L’idée de base est la même que pour l’exercice précédent, mais cette fois, du fait de l’alternance imposée fille / garçon, on raisonne sur le graphe biparti complet K6,6 (six filles et six garçons).
Ce graphe comprend 6 x 6 = 36 arêtes, et chaque cycle hamiltonien en nécessite 12. Il y a donc au maximum 3 solutions. En fait, trois solutions sont effectivement possibles (fi représente la i-ième fille, gi le i-ième garçon), par exemple :
( f1,g1,f2,g2,f3,g3,f4,g4,f5,g5,f6,g6) — (f1,g3,f2,g4,f3,g5,f4,g6,f5,g1,f6,g2) —
(f1,g5,f2,g6,f3,g1,f4,g2,f5,g3,f6,g4)
Exercice 22
Un groupe de huit personnes se retrouve pour dîner. Le graphe ci-contre précise les « incompatibilités d’humeur » entre les personnes de ce groupe (une arête reliant deux personnes indique que celles-ci s’entendent très modérément…).

Proposez un plan de table (la table est ronde) pour ce groupe en évitant de placer côte à côte deux personnes « incompatibles ».
Il s’agit cette fois de trouver des cycles hamiltoniens dans le complémentaire du graphe. En voici un : B,C,H,A,F,G,E,D.
