Contenus
ToggleAlgorithme de Gloushkov
L’algorithme de Gloushkov construit un automate non-déterministe acceptant l’ensemble des mots décrit par une expression rationnelle. Le nombre d’états de l’automate est proportionnelle à la taille de l’expression.
Les grandes étapes de l’algorithme de Gloushkov partant d’une expression rationnelle E sont les suivantes :
- Transformer l’expression E en une nouvelle expression E’ où chaque lettre apparaît au plus une fois dans E’.
- Construire un automate A’ acceptant l’ensemble des mots décrit par E’
- Transformer A’ en un automate A acceptant l’ensemble des mots décrit par E en remplaçant les symboles uniques de E’ par ceux d’origines
Etape 1 : lettres distinctes
La première étape de l’algorithme de Gloushkov consiste à rendre toutes les lettres distinctes dans l’expression. Chaque occurrence d’une même lettre est numérotée. L’expression E = (ab + b)* devient, par exemple, E’ = (ab0 + b1)*.
Prenons un exemple plus long : E = (a + b)*(abb + ε). Après renommage nous avons l’expression suivante : (x1 + x2)*(x3x4x5 + ε).
Il faut maintenant définir le groupe Premier contenant les symboles pouvant commencer un mot. Dernier le groupe contenant les symboles pouvant terminer le mot. Et un tableau de suivant définissant les symboles pouvant être suffixe d’un autre symbole.
Dans cet exemple nous avons :
- Premier = {x1,x2,x3}
- Dernier = {x1,x2,x5}
- Tableau des suivants :

Etape 2 : construction de l’automate
Soit E’ une expression rationnelle où toutes les lettres sont différentes. On construit un automate A’ de la façon suivante.
- L’ensemble des états est Q = {i} ∪ { a : a apparaît dans E’}
- L’état initial est l’état i
- Les états finaux sont Dernier(E’) auquel on ajoute i si ε ∈ E’
- Les transitions sont (i,a,a) pour a ∈ Premier(E’) et (a,b,b) pour (a,b) ∈ Suivant(E’)
Dans notre expression (x1 + x2)*(x3x4x5 + ε), nous construisons l’état initial i avec pour transition x1,x2,x3 vers les états respectifs x1, x2, x3.
Puis nous nous servons de la table des suivants pour créer les liens de type (a,b,b). Par exemple si nous prenons la première ligne nous avons les arcs suivants : (x1,x1,x1), (x1,x2,x2), (x1,x3,x3).
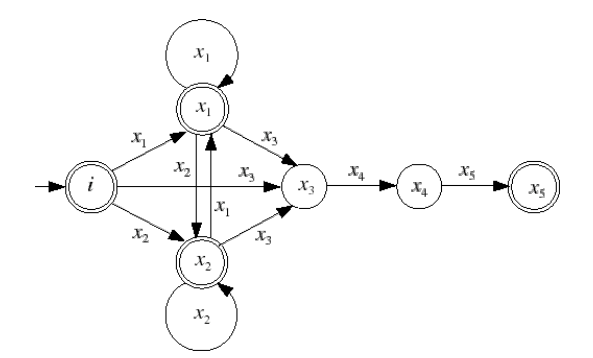
Pour terminer nous rajoutons les états terminaux {x1,x2,x5}. Ce qui donne au final l’automate suivant :