Automate à pile

Difficulté

Moyen 50%

Contenus

Les langages hors-contexte, décrits par des grammaires hors-contexte, sont reconnus (acceptés) par des automates à pile. De façon informelle, un automate à pile est un automate fini auquel on a ajouté une pile de capacité illimitée initialement vide. L’exécution d’un automate à pile sur un mot donné est semblable à celle d’un automate fini. Toutefois, à chaque étape, l’automate à pile consulte le sommet de sa pile et le remplace éventuellement par une suite de symboles.

Un automate à pile est un quintuplet A = (T, P, Q, M, S0) tel que :

T est le vocabulaire terminal,
P est le vocabulaire de pile (contenant en particulier un symbole initial de pile vide, noté ⊥),
Q est un ensemble fini d’états,
M est un ensemble de transitions,
S0 ∈ Q est l’état initial.

Le vocabulaire de pile contient l’ensemble des symboles qui pourront apparaître sur la pile, et n’est pas nécessairement distinct du vocabulaire terminal (on peut avoir T ∩ P ≠ ∅).

Une transition de l’automate à pile est semblable à celle d’un automate fini, à part qu’elle spécifie en plus la manipulation de la pile. Une transition de M est de la forme
(état, symbole_lu, sommet_pile) → (nouvel_état, action_sur_pile) tel que :

état et nouvel_état sont des états de Q,
symbole_lu est soit un symbole terminal de T, soit , signifiant que l’automate ne regarde pas le mot,
sommet_pile est soit un symbole de P, soit , signifiant que l’automate ne regarde pas le sommet de la pile,
action_sur_pile est soit :
“dépiler le symbole au sommet de la pile”, ou
“dépiler le symbole au sommet de la pile puis empiler une suite de symboles” ou
“empiler une suite de symboles”, ou
“ne rien faire”.

Le fonctionnement de l’automate A = (T, P, Q, M, S0) est défini de la façon
suivante :

Une configuration de l’automate est caractérisée par un triplet : (S, m, p) avec S ∈ Q, m ∈ T^∗ et p ∈ P^∗ c’est à dire, un état courant S, une suite m de symboles terminaux (correspondant à la fin du mot à analyser) et une suite p de symboles de pile (correspondant à l’état courant de la pile).

La configuration (S0, m0, p0) est dérivable en une étape de la configuration (S, m, p)
(noté (S, m, p) ⇒ (S0, m0, p0)) si : (S, u, v) → (S0, action_sur_pile) est une transition de M, m = u.m0 (le mot m à analyser commence par le symbole u), le symbole au sommet de la pile p est v. p0 est la pile obtenue après avoir effectué l’action de action_sur_pile sur la pile p.

Un mot w est accepté par l’automate à pile A si (S0, w, ⊥) ⇒ (S, ε, ⊥) où ⊥ est le symbole de pile vide. Le langage L(A) accepté par l’automate à pile A est l’ensemble des mots acceptés par A.

Autrement dit, un mot est accepté par l’automate s’il existe une suite de transitions à partir de l’état initial et pile vide, conduisant à la lecture entière du mot et à la pile à nouveau vide. A noter que certains automates à pile peuvent accepter sur états finaux sans pile vide. Par ailleurs, tout automate reconnaissant par état final possède un automate équivalent reconnaissant par pile vide.

Les automates à pile que nous avons définis acceptent un mot lorsqu’il existe une dérivation menant à une configuration où la pile est vide et le mot entièrement lu. Pour cette raison, ils sont appelés automates à pile acceptant sur pile vide. Une autre définition des automates à pile est celle des automates à pile acceptant sur état final. Un tel automate spécifie en plus un ensemble F ⊆ Q d’états finaux. Un mot est accepté s’il existe une dérivation menant à une configuration où l’état est final (la pile n’étant pas nécessairement vide).

Un automate à pile est dit déterministe si à toute situation ou configuration donnée ne correspond au plus qu’une transition.

Il existe des langages hors-contexte qui ne sont acceptés par aucun automate à pile déterministe. Les langages acceptés par les automates à piles déterministes forment donc une sous-classe des langages hors-contexte : la classe des langages hors-contexte déterministes.

Exemple

Voici un exemple d’automate à pile non déterministe. Soit l’automate à pile reconnaissant le langage des mots formés sur {a, b} et contenant le même nombre de a et de b : A = (T, P, Q, M, q) tel que : T = {a, b}, P = {a, b}, Q = {q} et la matrice de transition M suivante

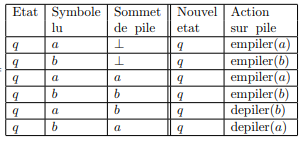
Le fonctionnement de cet automate sur le mot w = aabbabba est :

Comme pour les automates finis, on peut donner des automates à pile une représentation par graphe. Les arcs possèdent les informations suivantes :

symbole lu, symbole dépilé; symbole empilé.

Par exemple l’arc a, A; ε lira le symbole a à condition de pouvoir dépiler un symbole A en haut de la pile. A noté que ε ou λ représente « ne rien faire ».