Contenus
ToggleMinimisation d’un AFD
Théorème de Myhill-Nérode (minimisation d’un AFD). Soit L un langage rationnel. Parmi tous les AFD reconnaissant L, il en existe un et un seul qui a un nombre minimal d’états.
Avant de minimiser un AFD, il faut le compléter, c’est à dire rajouter un état poubelle comme l’état R sur le schéma ci-dessous.
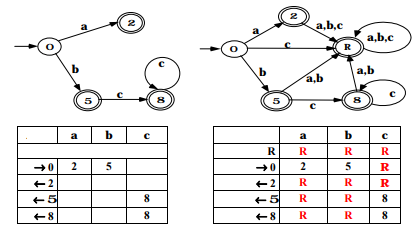
L’algorithme de minimisation est le suivant :
- Compléter l’AFD nommé D
- Construire une partition initiale ∏ contenant deux ensembles I et II d’états tel que ∏={I=(états terminaux d’acceptation de D), II=(autres états états de D)}
- Pour chaque état de D faire
- Construire la table de transition
- Marquer les états de départ et d’arrivées en fonction de leur groupe de ∏
- Si des états du même groupe de ∏ ont des comportements divergeant
- Séparer les états dans un nouveau groupe (III par exemple) – de préférence ne faire qu’une séparation par itération.
- Retourner à 3
- Fin : les nouveaux états sont les groupes de ∏
Exemple
Reprenons l’exemple de l’AFD ci-dessus. Il est bien déterministe comme le montre la table de transition.
Regardons la table de transition à l’étape 3 :
| a | b | c | |
| 0(I) | 2(II) | 5(II) | R(I) |
| 2(II) | R(I) | R(I) | R(I) |
| 5(II) | R(I) | R(I) | 8(II) |
| 8(II) | R(I) | R(I) | 8(II) |
| R(I) | R(I) | R(I) | R(I) |
Nous remarquons quand dans le groupe I, le comportement de O et de R divergent, nous allons donc les séparer en deux groupes: I=(0) et III=(R)
Voici la nouvelle table de transition :
| a | b | c | |
| 0(I) | 2(II) | 5(II) | R(III) |
| 2(II) | R(III) | R(III) | R(III) |
| 5(II) | R(III) | R(III) | 8(II) |
| 8(II) | R(III) | R(III) | 8(II) |
| R(III) | R(III) | R(III) | R(III) |
Nous remarquons quand dans le groupe II, le comportement de 2 et de 5, 8 divergent, nous allons donc les séparer en deux groupes: II=(5, 8) et IV=(2)
Voici la nouvelle table de transition :
| a | b | c | |
| 0(I) | 2(IV) | 5(II) | R(III) |
| 2(IV) | R(III) | R(III) | R(III) |
| 5(II) | R(III) | R(III) | 8(II) |
| 8(II) | R(III) | R(III) | 8(II) |
| R(III) | R(III) | R(III) | R(III) |
On n’observe plus de divergence entre les groupes, nous pouvons donc effectuer la table de transition avec l’AFD minimisé donnant la table de transition suivante :
| a | b | c | |
| I | IV | II | III |
| IV | III | III | III |
| II | III | III | II |
| III | III | III | III |
L’état inital est I (en rapport à son équivalent dans D), et les états terminaux de l’automate sont II et IV (en rapport à leurs équivalents dans D).
Autre exemple
Prenons l’automate suivant :

La phase d’initialisation permet d’obtenir le groupe non terminal I et le groupe terminal II :
| A | B | C | D | |
| Init | I | II | I | II |
Regardons les transitions pour chaque état selon les groupes I et II :
| Alphabet | A | B | C | D |
| a | II | II | I | II |
| O | I | II | I | II |
Puis on effectue la séparation des ensembles. Deux états sont dans un même ensemble s’ils étaient déjà dans le même ensemble et si les transitions mènent dans les mêmes ensembles. Dans cet exemple, B et D se comportent exactement de la même manière, donc ils restent ensemble. Par contre, A et C qui faisaient partie du même ensemble se comportent différemment sur le symbole « a ». Par conséquent, l’ensemble noté I se divise en deux. Nous obtenons donc :
| A | B | C | D | |
| Init | I | II | I | II |
| a | II | II | I | II |
| 0 | I | II | I | II |
| Séparation 1 | I | II | III | II |
La situation courante (la ligne Bilan 1) est différente que la situation de départ. Donc il faut recommencer.
| A | B | C | D | |
| Init | I | II | I | II |
| a | II | II | I | II |
| 0 | I | II | I | II |
| Séparation 1 | I | II | III | II |
| A | II | II | III | II |
| 0 | III | II | III | II |
| Séparation 2 | I | II | III | II |
La ligne « Séparation 2 » est identique à la ligne « Séparation 1 ». Par conséquent, dans chacun des ensembles restants, les états ne sont pas distinguables (ils se comportent exactement de la même manière et sont donc « redondants »).
Nous pouvons donc construire le nouvel automate en associant un état à chaque ensemble. Les transitions sont indiquées par le tableau. L’état initial est celui contenant l’état initial de l’automate de départ : ici I contient l’état A, état initial. Les états finaux sont les états dont l’ensemble correspondant contient au moins un état final : ici, II contient B et D qui sont finaux.
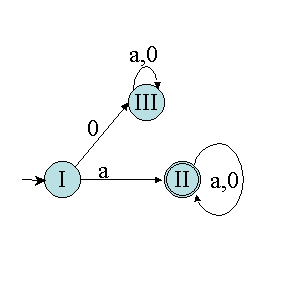
Pour l’instant, nous avons « fusionné » les états indistinguables. Il faut maintenant supprimer tous les états inutiles restant. Dans notre exemple, l’état III est un état stérile (non terminal et sans transition), donc inutile. Il faut donc le supprimer. D’où l’automate déterministe minimal de la figure suivante :

