Aide à la décision 101

Aide à la décision

Tout problème industriel consiste, sous certaines conditions, à maximiser un profit ou minimiser les dépenses. Dans ce contexte, profit et dépenses ne font pas toujours référence à une variable monétaire, cela peut aussi se traduire par le temps, la distance ou autres.

Bien souvent, le problème est énoncé de manière brute, c’est-à-dire par un texte ou un cahier des charges. L’industriel n’était pas expert dans le domaine de l’écriture d’un problème mathématique, le cahier des charges comprend toutes sortes de données, utiles ou non pour sa modélisation.

Même dans le cadre où vous êtes vous-même commanditaire, il se peut que vous ne connaissiez pas l’étendue de votre problème, et que vous découvrez au cours de l’eau les différentes contraintes et variables à faire face.

Un autre problème s’annonce une fois la modélisation mathématique effectuée : quel outil informatique utilisé pour résoudre ce problème ? quel algorithme choisir ? sa simulation ? sa complexité ? son optimalité ?

Construire et résoudre un problème industriel demandent donc de la rigueur, de la souplesse d’esprit et de suivre une démarche de modélisation précise.

Optimisation et aide à la décision

Un problème D est de décision si la réponse est binaire : Oui ou Non. On note Oui(D) l’ensemble des instances auxquelles on répond Oui.

Prenons le problème de décision suivant : soit un graphe G pondéré, existe-t-il un arbre couvrant ? Oui(D) = {sous-graphe de G connexe non cyclique}. Le problème : existence d’un arbre couvrant de poids ≤ k est aussi un problème de décision. Le problème d’optimisation est de rechercher la valeur k de telle sorte qu’elle soit minimale.

Afin de mieux comprendre les deux notions, nous allons prendre un exemple : Vous souhaitez faire un tour d’Europe, en visitant un certain nombre de villes dans un laps de temps de 6 mois. De plus, vous souhaitez rester une certaine durée dans chaque lieu afin de pouvoir visiter les zones touristiques et admirer le paysage.

Ce genre de problème a différentes façons d’être modélisation en fonction de ce qu’on souhaite faire : être le plus rapide, favoriser les zones densément touristiques, etc. Il faut sélectionner une décision parmi un ensemble de décision possible de manière à optimiser le critère choisi.

La modélisation comporte une recherche de minimum ou de maximum, il s’agit donc d’une optimisation. Les problèmes d’aide à la décision contiennent tous les trois points suivants :

• Le type de décision : ce que l’on veut faire (ici nous cherchons une optimisation)
• Les décisions possibles : ce que l’on peut faire (le domaine de définition)
• Le critère de sélection : comment on choisit (la modélisation du problème).

Le problème étudié se place dans un certain contexte qui sera traduit en paramètres. Toutes les relations entre ces derniers sont représenté dans le modèle. Ce dernier peut soit prendre le forme d’un modèle mathématique, soit un graphe.

La modélisation n’est qu’une représentation schématique du problème, seuls les éléments jugés pertinents sont retenus dans la construction de la décision. Elle procède par simplifications et omissions.

L’environnement du modèle peut aussi jouer un rôle. Que ce soit déterministe ou avec incertitude, il est présent via des lois de probabilité, du stochastique, etc. au sein des contraintes.

Le critère de sélection peut amener à des solutions différentes en fonction du paramètre mis en avant. Dans certains cas, le modèle ne présente qu’un seul critère de sélection, on parle alors de recherche opérationnelle.

Tous les modèles sont constitués de trois composants de base:

• Les variables de résultat sont des sorties. Le reflètent le niveau d’efficacité du système. Ce sont des variables dépendantes.
• Les variables de décision décrivent des actions alternatives.
• Les variables incontrôlables sont des facteurs qui affectent le résultat mais ne sont pas sous le contrôle du décideur. Soit ces facteurs sont fixes ou ils peuvent varier.

Les composants sont reliés entre eux par des expressions mathématiques dans une structure de modèles quantitatifs. Un principe de choix est un critère qui décrit l’acceptabilité d’une solution d’approche.

Un modèle peut être un modèle normatif ou un modèle descriptif. Dans le premier, la solution choisie est manifestement la meilleure de toutes les alternatives possibles. Pour la trouver, il faut examiner toutes les alternatives et prouver que celle qui est sélectionnée est effectivement la meilleur (on parle d’optimisation). Les modèles descriptifs étudient des actions alternatives sous différentes configurations d’entrées et de processus. Toutes les alternatives ne sont pas vérifiées, seul un ensemble donné le sont.

Solution et aide à la décision

Une fois que le modèle a été créé et qu’une solution a été trouvé, il est important de l’analyser afin de valider le modèle. Ce dernier n’était qu’une représentation schématique du problème, il peut ne pas convenir à l’objectif recherché. Une solution met en évidence la validité des choix de décision et des choix du modèle. Seul le décideur / commanditaire peut valider l’approche effectuée.

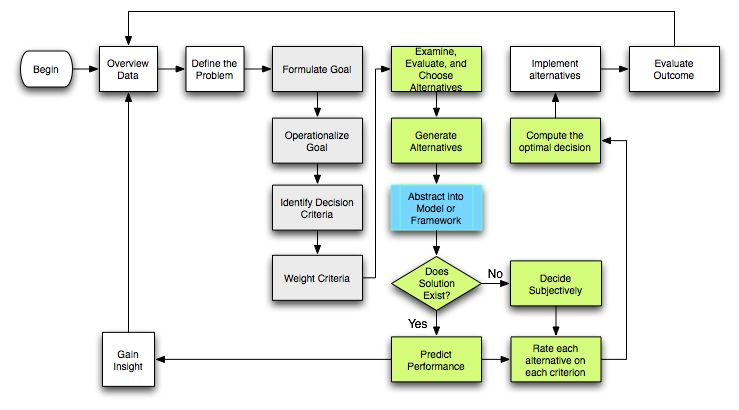
Le schéma du processus d’aide à la décision est le suivant :