Modélisation mathématique

Modélisation mathématique

La modélisation mathématique est à la base de tout le travail ingénierie. Une modélisation mathématique se caractérise par trois notions :

1. La présence de choix, à faire parmi un ensemble fini (notion que l’on peut rapprocher de la théorie des probabilités)
2. Un principe de contraintes définissant l’ensemble fini des choix
3. Un principe d’évaluation des choix disponibles

Modélisation mathématique d’un problème

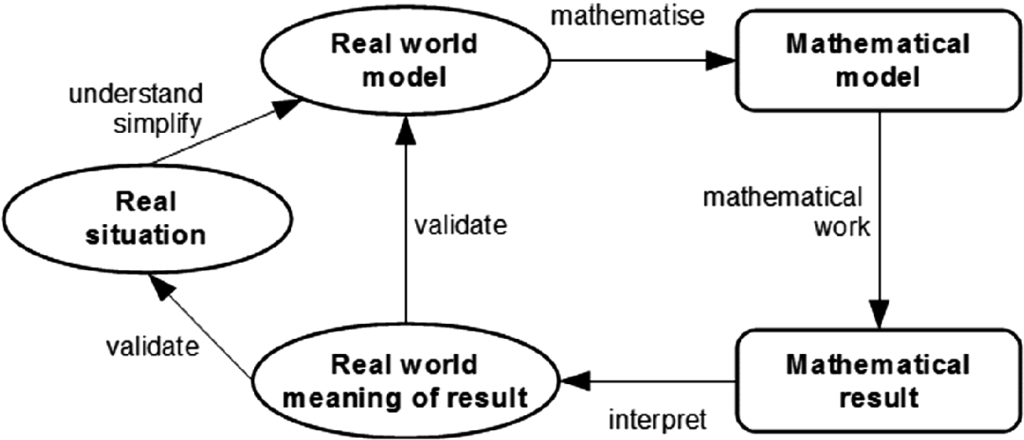
Les quatre étapes de la modélisation mathématique d’un problème industriel sont les suivantes :

• Quelles sont les données du problème ? récolter les données du problème, comprendre le problème;
• Comment modéliser le problème ? les trois points de l’aide à la décision
  • Quelles décisions doit-on prendre ? sélectionner/placer des objets, définir un ordre ou une quantité, choisir un événement, effectuer une opération particulière;
  • Quels sont les contraintes du problème ? respecter des capacités ou des contraintes de précédence;
  • Quel est l’objectif recherché ? maximiser un profit, minimiser des coûts ou une quantité;
• Quelle est la complexité de ce problème ? polynomiale, Np, Np-difficile;
• Comment résoudre le problème ? concevoir des algorithmes (exacts vs approchés) donnant des solutions réalisables/optimales, développer des méthodes alternatives ou hybrides

En fonction de la modélisation mathématique, le modèle peut aussi servir de simulation. Il est alors possible de voir l’impact de certaines décisions dans un contexte différent de celui étudié (comme l’étude de sensibilité du simplexe).

Prise de décision et modélisation mathématique 

La prise de décision lors de la modélisation mathématique implique trois phases majeures suivies par la phase de validation:

• Collecte d’informations: Examiner et identifier le problème (variables, fonctions, valeurs, etc.).
  • Identification du problème: Identification des buts et objectifs organisés liés à un problème. Pour déterminer si un problème existe, identifiez ses symptômes, déterminez leur ampleur et définissez-le explicitement. Certains problèmes peuvent survenir lors de la collecte et de l’estimation des données comme le manque de données, des données imprécises ou inexactes, une mauvaise estimation, une surcharge d’information, des données simulées, etc.
  • Classification du problème: La classification du problème est le placement d’un problème dans une catégorie définissable. Cela conduit à une approche par une solution standardisée.
  • Décomposition des problèmes: De nombreux problèmes complexes peuvent être divisés en sous-problèmes. Certains problèmes non structurés peuvent avoir des sous-problèmes très structurés.
• Conception: Construire un modèle qui représente le système.
  • Comprendre le problème: La modélisation implique l’abstraction du problème à des formes quantitatives et / ou qualitatives.
  • Un modèle est construit, testé et validé: Pour un modèle mathématique, les variables sont identifiées et les relations entre elles sont établies. Tous les modèles sont constitués de trois composantes de base: les variables de décision, les variables incontrôlables et les variables de résultat. Les relations mathématiques lient ces composants ensemble. Dans un modèle non quantitatif, les relations sont symboliques ou qualitatives.
• Choix: Pour sélectionner une solution au modèle.
  • Recommandation d’une solution: Lorsque le problème est résolu, une solution est choisie en fonction du modèle. Celle-ci est recommandée sur l’ensemble des solutions.
  • Evaluation d’une solution: L’évaluation est possible si les variables de résultat donnent une solution quantitative. Une relation de préférence sur l’ensemble de la solution donne un ordre: f (a) ⪯ f (b) signifie que f (b) est meilleur ou égal à f (a) où a, b sont des variables et f (.) est une fonction mathématique basée sur les variables de résultat. b est la meilleure solution ssi: f (x) ⪯f (b) pour tout x dans l’ensemble de la solution.
• Implémentation: Implémenter un logiciel pour résoudre n’importe quelle instance de la modélisation mathématique.
  • Implémentation classique/itérative: les algorithmes itératifs utilisent des constructions répétitives comme des boucles et parfois des structures de données supplémentaires comme des piles pour résoudre les problèmes donnés.
  • Récursivité: un algorithme récursif est un algorithme qui fait référence à lui-même à plusieurs reprises jusqu’à ce qu’une condition de terminaison corresponde.
  • Logique: un algorithme logique est composé d’une composante logique et d’une composante de contrôle.
  • Déterministe ou non déterministe: les algorithmes déterministes résolvent le problème avec une décision exacte à chaque étape de l’algorithme, tandis que les algorithmes non déterministes résolvent les problèmes par « devinettes ». Un algorithme déterministe est un algorithme qui, donné une entrée particulière, produira toujours la même sortie.
  • Exact ou approximatif: Alors que de nombreux algorithmes atteignent une solution exacte, les algorithmes d’approximation recherchent une approximation proche de la vraie solution. Quand il n’est pas possible de trouver la meilleure solution en temps humain, on peut chercher une solution approchée par des algorithmes moins complexes.
  • Série, parallèle ou distribué: ces implémentations dépendent des architectures informatiques, c’est-à-dire du nombre de processeurs qui peuvent travailler sur un problème en même temps, et comment décomposer l’ensemble du processus en processus indépendants.
  • Paradigme: Brute-force; Diviser et conquérir; Programmation dynamique; Chercher; Randomisé; Réduction. Ensuite, nous devons vérifier la terminaison, la correction et la complétude de l’algorithme.
• Validation: Pour valider le logiciel s’il présente un temps de calcul raisonnable et une bonne solution.
  • La complexité du meilleur cas: C’est la complexité pour résoudre le problème pour la meilleure entrée de taille n.
  • La complexité du pire des cas: C’est la complexité pour résoudre le problème pour la pire entrée de taille n.
  • Complexité moyenne des cas: C’est la complexité pour résoudre le problème en moyenne. Cette complexité n’est définie que par rapport à une distribution de probabilité sur les entrées. Par exemple, si toutes les entrées de la même taille sont supposées être également susceptibles d’apparaître, la complexité moyenne des cas peut être définie par rapport à la distribution uniforme sur toutes les entrées de taille n.

Le schéma suivant présente le processus de modélisation mathématique :