Contents
ToggleCorrected exercises about shortest path problems
This page presents several corrected exercises on shortest path problems. The exercises are mainly about shortest path for one source and shortest path from many sources.
Exercise 1
The air company Europa serves various European cities. The table below gives against the flight times between these cities.
• How to determine the fastest route between two cities?
• How to modify the previous method to take into account the duration of stopovers in different cities?
| TO | B | VS | D | E |
TO |
| 1h30 | 2h00 |
| 2h15 |
B | 1h40 |
|
|
| 3h00 |
VS | 2h20 |
|
| 2h55 |
|
D |
|
| 3h20 |
| 1h05 |
E | 2h25 | 3h10 | 1h10 |
|
|
Simply draw the graph, whose vertices are cities and arcs the routes of the company, valuated each arc length of the corresponding flight. A shortest path algorithm then solves the problem.
To take into account the duration of stopovers, two methods are possible: Edit the previous algorithm, including in arcs the cost of stopover OR: each vertex is duplicated; an arc between them is the stopover of the corresponding city.

Exercise 2
We want to build a new plant in the following network, nodes are places and links represent costs to send energy from one place to another:

Based on Dijkstra algorithm, proposes a method to find the best place to build the plant, and then solve the problem with your method. Solve the problem with Floyd–Warshall algorithm.
We have to compute Dijkstra for each node (at source node). Once the tree of paths is created, sum up the cost of all paths from any node to the source node (sum the last shortest paths array). The best place is the minimum total weight of all Dijkstra occurrences. With Floyd-Warshall, the pseudo-closure matrix contains all arrays, just sum the inputs of each array and find the minimum.
Exercise 3
A robot moves in the following environment. It starts from the node labeled start and needs to reach the node labeled end. The environment is continuous and the scale is supplied on the figure. Considering the robot is a point, what is the shortest path from Start to End.
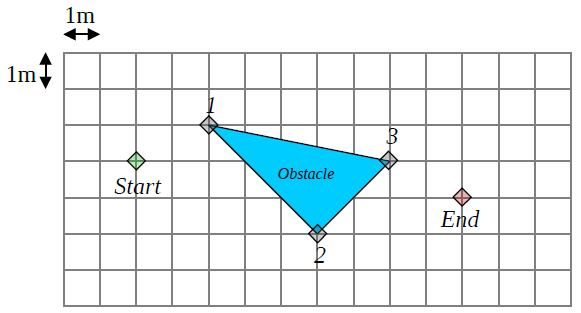
Compute the Euclidian distance between the nodes. Draw the graph and apply Dijsktra's algorithm to find the shortest path from the node Star to the node End. Then draw the path on the figure.
Shortest path | Start | 1 | 2 | 3 | End |
Init | 0 | inf | inf | inf | inf |
Start | – | sqrt 5 | sqrt 29 | inf | inf |
1 | – | – | sqrt 29 | sqrt 5+ sqrt 26 | inf |
2 | – | – | – | sqrt 5+ sqrt 26 | sqrt 29 + sqrt 17 |
3 | – | – | – | – | sqrt 29 + sqrt 17 |
The shortest path is Start-2-End.
Exercise 4
Considering the graph on exercise 1, edges are directed from left to right (or up to down) and weights are decreased by 4. How to find a minimal path from A to F? Solve it.
Exercise 5
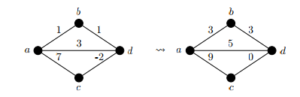
(a) Calculate the shortest path from s to all other vertices by using the Dijkstra algorithm. Determine the shortest path tree.
(b) Is the shortest path tree unique?
(c) Now change the weight of the edge (3, 4) to −2. Show that the Dijkstra algorithm does not work in this case.

(a) The solution is given by the following picture. The numbers next to vertices are the distances to the starting vertex and crossing out a number means that there has been an update. The numbers in squares indicate the final distances (shortest distances).

(b) No shortest path tree is not unique. By substituting the edge (s, 3) with the edge (1, 2) one gets another shortest path tree.
(c) The Dijkstra algorithm will give the same solution as in part (a) although the path (s, 1, 2, 3, 4) (dist 5) has a shorter distance than the path (s, 1, 4) ( dist 6). This is what happens: After visiting the vertices s, 1, 2 the algorithm will look for the shortest path to a not yet visited vertex. This will be vertex 4 with distance 6. After visiting vertex 4 the algorithm will not make an update on vertex 4 because it was already visited and for this reason not find the shortest path (distance 5).
Exercise 6
A man has to transport a wolf, a goat and a cabbage to the other side of a river. He has one boat to do this but it is so small that he can only take one of the three things with him each time. Is it possible to bring all three things to the other side of the river safely? Notice that the wolf and the goat or goat and the cabbage must never be on the same side of the river without surveillance of the man. At least the wolf is not vegetarian and does not like to eat cabbage.
We construct a graph for this problem where every legal state is represented by a vertex in the graph and look for a shortest path in that graph. So let S = {M, W, G, C} where M, W, G, C are the man, the wolf, the goat and the cabbage. A state for this problem is a pair (X, Y) where {X, Y} is a partition of S. The elements in X are still on the starting side of the river and the elements in Y are already on the other side. A state is a legal state if W, G ∈ X, Y ⇒ M ∈ X, Y and G, C ∈ X, Y ⇒ M ∈ X, Y, you may not leave alone the cabbage and the wolf or the goat and the cabbage without surveillance. Now construct a graph G = (V, E) which has a vertex for every legal state of this problem. We have the directed edge (v1, v2) ∈ E if we can get from the state v1 = (X1, Y1) to the state v2 = (X2, Y2) by just one boat trip across the river. All edges get the weight ce = 1. Now the problem can be solved by calculating the shortest path from the state (vertex) s = (S, 😉 to the state (vertex) t = (;, S). We get 7 as the solution for the shortest path.
Exercise 7
Consider the following modification of the Dijkstra's algorithm to work with negative weights: Determine the smallest weight c in ℤ in the weighted graph G = (V, E, w), ie, the edge e st w (e) = c. Then for all edges f in E set w '(f): = w (f) - c. Then G '= (V, E, w') has no negative weights. Does this version of the algorithm work correctly on this type of graph? Prove your claim.
Now we claim that DJP does not work correctly on G 'because this modification does not maintain the shortest path property, ie, (-c) is a positive number, so you add it n times for an n-path. The following counter-example proves this: