Edmonds-Karp algorithm

Contents

The Edmonds-Karp algorithm has a running time of O(VE²), it is faster than the algorithm of Ford-Fulkerson for dense graphs, i.e. a graph containing a large number of edges (or arcs) depending on the number of vertices.

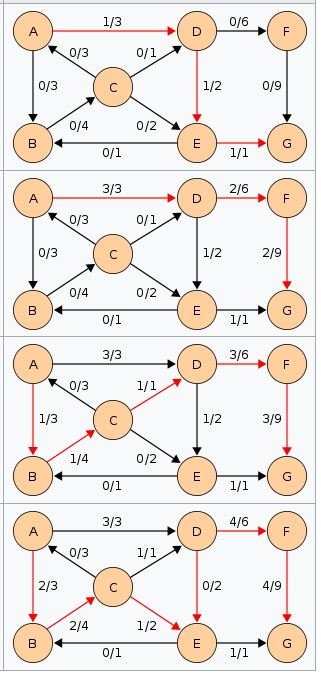
The Edmonds-Karp algorithm is identical to the Ford-Fulkerson algorithm, except for the search order used to determine an increasing path. The path found must be the shortest path that has a positive capacity. Such a path can be found by a width course, assuming that the arcs all have unit length. Note that the length of the increasing path increases with each iteration.

Code from Wikipedia
algorithm EdmondsKarp
    input: C [1..n, 1..n] (capacity matrix)
        E [1..n, 1 ..?] (lists of neighbors)
        s             (source)
        t             (well)
    output: f             (maximum flow value)
        F             (matrix giving a valid flow of maximum value)
    f: = 0 (the initial flow is zero)
    F: = array(1..n, 1..n) (the residual capacity from u to v is C[u,v] - F[u,v])
    forever
        m, P: = BreadthFirstSearch (C, E, s, t, F)
        yew m = 0
            break
        f: = f + m
        (Backtrack and note the flow)
        v: = t
        while v ≠ s u: = P [v] F [u, v]: = F [u, v] + m F [v, u]: = F [v, u] - m v: = u
    return (f, F)

algorithm BreadthFirstSearch
    input: It's f
    output: M [t]          (capacity of the path found)
        P             (parents table)
    P: = array(1..n)
    for u in 1..n P [u]: = -1 P [s]: = -2 (to ensure that the source is not rediscovered) 
    M: = array(1..n) (capacity of the path found to the node)
    M [s]: = ∞ Q: = tail () Q.push (s)
    while Q.size ()> 0 u: = Q.pop ()
        for v in E [u]
            yew C [u, v] - F [u, v]> 0 and P [v] = -1 P [v]: = u M [v]: = min (M [u], C [u, v] - F [u, v])
                yew v ≠ t Q.push (v)
                else
                    return M [t], P
    return 0, P