Contenus
ToggleFonction de similarité
Un concept alternatif à celui de la distance est la fonction de similarité (mesure du cosinus, mesure de corrélation de Pearson, Mesure de Jaccard étendue, mesure du coefficient de Dice) s(x_i, x_j) qui compare les deux vecteurs x_i et x_j. Cette fonction doit être symétrique (à savoir s(x_i, x_j) = s(x_j, x_i)) et avoir une grande valeur lorsque x_i et x_j sont en quelque sorte «similaires» et constituent la plus grande valeur pour des vecteurs identiques.
Une fonction de similitude où la plage cible est [0,1] est appelée fonction de similitude dichotomique. En fait, les méthodes de calcul de «distances» dans le cas des attributs binaires et nominaux peuvent être considérées comme des fonctions de similitude plutôt que comme des distances.
Mesure du cosinus
Lorsque l’angle entre les deux vecteurs est une mesure significative de leur similitude, le produit intérieur normalisé peut être une mesure de similitude appropriée:
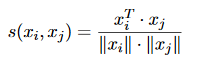
Mesure de corrélation de Pearson
La corrélation de Pearson normalisée est définie comme (avec x̄ la valeur caractéristique moyenne de x sur toutes les dimensions):

Mesure de Jaccard étendue
La mesure de Jaccard étendue a été présentée par Strehl et Ghosh en 2000 et elle est définie comme:

Mesure du coefficient de Dice
La mesure du coefficient de Dice est similaire à la mesure de Jaccard étendue et elle est définie comme suit:

