Contenus
ToggleMesures de distance pour les attributs binaires
De nombreuses méthodes de partitionnement utilisent des mesures de distance pour déterminer la similitude ou la dissemblance entre n’importe quelle paire d’objets (comme des attributs binaires). Il est courant de désigner la distance entre deux instances x_i et x_j comme: d (x_i, x_j). Une mesure de distance valide doit être symétrique et obtient sa valeur minimale (généralement zéro) dans le cas de vecteurs identiques. La mesure de distance est appelée mesure de distance métrique si elle satisfait également aux propriétés suivantes :
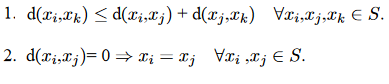
Dans le cas d’attributs binaires, la distance entre les objets peut être calculée sur la base d’un tableau de contingence. Un attribut binaire est symétrique si ses deux états ont la même valeur. Dans ce cas, l’utilisation du coefficient d’appariement simple peut évaluer la dissimilarité entre deux objets :

où q est le nombre d’attributs égaux à 1 pour les deux objets; t est le nombre d’attributs égaux à 0 pour les deux objets; et s et r sont le nombre d’attributs qui sont inégaux pour les deux objets.
Un attribut binaire est asymétrique, si ses états ne sont pas également importants (le résultat positif est généralement considéré comme plus important). Dans ce cas, le dénominateur ignore les correspondances négatives sans importance (t). C’est ce qu’on appelle le coefficient de Jaccard :

