Chaines de Markov en temps continu

Difficulté

Moyen 50%

Contenus

Dans le cas du temps discret, nous observons les états sur des moments instantanés et immuables. Dans le cadre des chaines de Markov en temps continu, les observations se dont de façon continu, c’est à dire sans interruption temporelle.

Temps continu

Soient M + 1 états mutuellement exclusifs. L’analyse débute au temps 0 et le temps s’écoule de façon continue, on nomme X(t) l’état du système au temps t. Les points de changement d’états t_i sont des points aléatoires dans le temps (ils ne sont pas nécessairement entiers). Il est impossible d’avoir deux changements d’états en même temps.

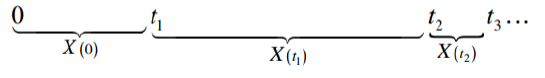
Considérons trois points consécutifs dans le temps où il y a eu un changement d’états r dans le passé, s à l’instant présent et s + t dans le futur. X(s) = i et X(r) = l . Un processus stochastique en temps continu à la propriété de Markov si :

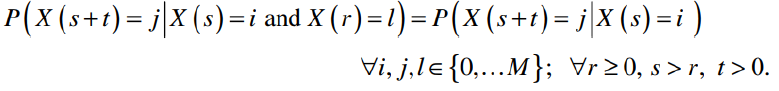
Les probabilités de transition sont stationnaires puisqu’elles sont indépendantes de s. On note p_ij(t) = P(X(t) = j , X(0) = i ) la fonction de probabilité de transition en temps continu.

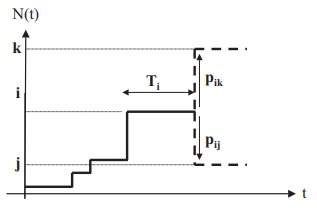
Notons T_i une variable aléatoire dénotant le temps passé dans l’état i avant de se déplacer vers un autre état, i∈{0, …,M}. Supposons que le processus entre dans l’état i au temps t’ = s. Alors pour une durée t > 0, T_i > t ⇔ X(t’ = i ), ∀t’∈[s, s + t].

La propriété de stationnarité des probabilités de transition entraîne : P(T_i > s + t, T_i > s) = P(T_i > t). La distribution du temps restant d’ici la prochaine sortie de i par le processus est la même quel que soit le temps déjà passé dans l’état i . La variable T_i est sans mémoire. La seule distribution de variable aléatoire continue ayant cette propriété est la distribution exponentielle.

La distribution exponentielle T_i possède un seul paramètre q_i et sa moyenne (espérance mathématique) est R[T_i ] = 1/q_i. Ce résultat nous permet de décrire une chaîne de Markov en temps continu d’une façon équivalente comme suit :

La variable aléatoire T_i a une distribution exponentielle de paramètre λ
quand le processus quitte l’état i, il passe à l’état j avec une probabilité p_ijtelle que (similaire à une chaîne de Markov en temps discret) :
le prochain état visité après i est indépendant du temps passé dans l’état i.
La chaîne de Markov en temps continu possède les mêmes propriétés de Classe et d’Irréductibilité que les chaînes en temps discret.

Voici quelques propriétés de la loi exponentielle :

Modèle de durée

Ainsi, si on considère μ_i le paramètre de la variable aléatoire exponentielle associé à l’état i, nous pouvons représenter la chaîne de Markov à temps continue comme suit :

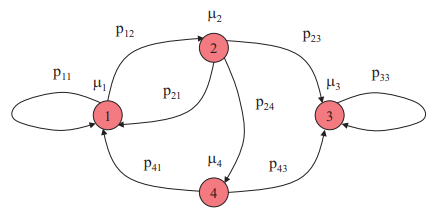
Nous voyons bien la chaîne de Markov à temps discret incluse, d’où la possibilité d’effectuer une étude du modèle discret. A noter qu’il n’existe pas de notion de périodicité dans ce cadre.

Si l’on considère qu’on se déplace de l’état i à l’état j après un temps T_ij et que l’on considère ce temps comme une variable aléatoire exponentielle de taux μ_ij, alors il est possible d’écrire la chaîne de Markov en temps continu sous un modèle de durée :

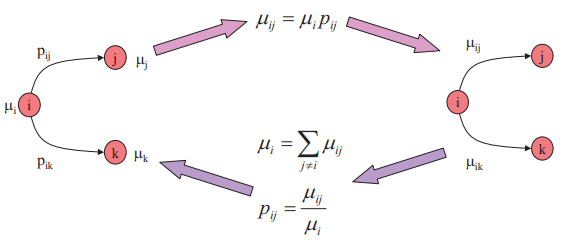
Attention, il existe un grand changement entre le côté stochastique du mouvement d’un état à un autre et le côté continue dans le temps. Il est important de comprendre que la matrice de transition d’une chaîne de Markov en temps continue est toujours un modèle de durée.

La matrice de transition d’un modèle de durée à les propriétés suivantes :

Cette matrice est appelé le générateur infinitésimale.

Ainsi, à partir du graphe de Markov discret suivant (la loi exponentielle est la même dans les trois états) :

Il est possible d’obtenir le modèle de temps suivant :