Critères de récurrence et transience

Critères de récurrence et transience

Nous allons étudier une seconde classification des états dépendant du type de comportement de la chaîne (les critères de récurrence et transience).

Soit x un état de la chaîne, nous notons le temps d’atteinte de x, noté T_x, le premier instant où x est visité après le départ. par convention, le temps d’atteinte est infini si nous n’atteignons jamais x. La formule est la suivante (nous utiliserons les notations classiques pour les probabilités) :

Si la chaîne part de l’état x, nous employons le terme de temps de retour.

Un état x est dit récurrent si :

L’état x est dit transient ou transitoire sinon, c’est à dire quand :

 

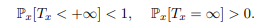
Un état est récurrent si nous sommes sûr d’y revenir, il est transient s’il existe une probabilité non nulle de ne jamais y revenir, et donc de le quitter définitivement.

Une classe d’équivalence est dite récurrente, respectivement transiente, si un de ses sommets est récurrent, resp. transient.

Soit x un état quelconque appartenant à la classe de récurrence C. Supposons
qu’il existe y ∉ C tel que x → y et montrons que l’on a une contradiction. Remarquons d’abord que y ne conduit à aucun sommet de C, car sinon on aurait y → x et donc x ↔ y et y ∈ C. De plus, on a :

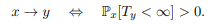
Or, la probabilité de ne pas revenir en x est bornée inférieurement par la probabilité d’aller en y en temps fini (vu que y ne conduit à aucun état de C). Ainsi, nous avons la relation suivante :

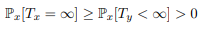
Ce qui est une contradiction avec x récurrent. Nous voyons qu’une classe récurrente est fermée, mais la réciproque est fausse en général, elle est tout de même vérifiée si cette classe est de cardinal fini.