Contenus
ToggleExercices Corrigés sur Analyse exploratoire des données
Cette page présente deux exercices corrigés et détaillés avec le code python sur l’analyse exploratoire des données.

Exercice 1
Considérons un échantillon aléatoire de finisseurs du marathon de New York en 2002. Cet ensemble de données se trouve dans le package UsingR. Chargez la bibliothèque, puis chargez l’ensemble de données nym.2002.
library(dplyr)
data(nym.2002, package="UsingR")Utilisez des boîtes à moustaches et des histogrammes pour comparer les temps d’arrivée des hommes et des femmes. Lequel des résumés décrit le mieux la différence ?
data(nym.2002, package="UsingR")
male <- nym.2002 %>% filter(gender == 'Male')
female <- nym.2002 %>% filter(gender == 'Female')
mypar(1,2)
hist(female$time, xlim = c(100,600))
hist(male$time, xlim = c(100,600))
Les deux histogrammes ont une distribution similaire (inclinée vers la droite). Mais le centre de l’histogramme semble être différent. Nous pouvons le vérifier en calculant la différence absolue entre la moyenne et la médiane.
abs(mean(male$time) - mean(female$time))## [1] 23.11574abs(median(male$time) - median(female$time))## [1] 21.70833Il y a une différence d’environ 21-23 minutes entre les hommes et les femmes. Les hommes et les femmes ont des distributions similaires asymétriques vers la droite, les premières 20 minutes étant décalées vers la gauche.
Utilisez dplyr pour créer deux nouvelles trames de données : hommes et femmes, avec les données pour chaque sexe. Pour les hommes, quelle est la corrélation de Pearson entre l’âge et le temps pour terminer ?
plot(male$age, male$time, main = 'male')
cor(male$age, male$time)## [1] 0.2432273Pour les femmes, quelle est la corrélation de Pearson entre l’âge et le temps pour terminer ?
plot(female$age, female$time, main = 'female')
cor(female$age, female$time)## [1] 0.2443156Si nous interprétons ces corrélations sans visualiser les données, nous conclurions que plus nous vieillissons, plus nous courons des marathons lentement, quel que soit le sexe. Examinez les diagrammes de dispersion et les boîtes à moustaches des heures stratifiées par tranches d’âge (20-24, 25-30, etc.). Après avoir examiné les données, quelle est la conclusion la plus raisonnable ?
groups_m <- split(male$time, floor(male$age/5)*5) # 10-14, 15-19, etc
groups_f <- split(female$time, floor(female$age/5)*5) # 10-14, 15-19, etc
mypar(1,2)
boxplot(groups_m)
boxplot(groups_f)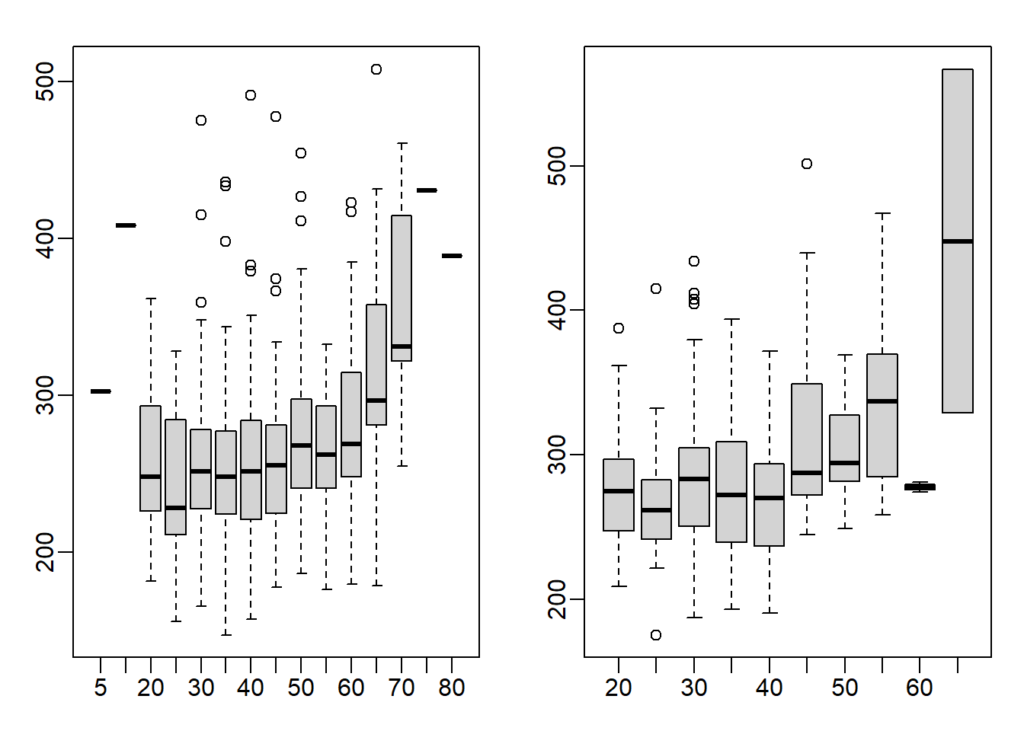
C’est une question délicate car la question vous demande de stratifier les données en groupes. La stratification peut être réalisée via la fonction de split. Pour que chaque groupe ait une plage de 5 (ex. 25-30), tous les nombres d’âge devront être arrondis vers le haut ou vers le bas afin que les nombres résultants soient divisibles par 5. J’ai arrondi les nombres vers le bas en utilisant la fonction plancher.
Par conséquent, 40 représente la tranche d’âge 40-44 . Vous pouvez également utiliser la fonction de plafond pour stratifier les données, qui seront ensuite arrondies. Ainsi, 45 représente 41-45 groupe d’âge. Dans l’exemple ci-dessous, l’âge de 42 ans est classé à l’aide des fonctions de plancher et de plafond.
floor(42/5)*5 ## [1] 40ceiling(42/5)*5## [1] 45Les temps d’arrivée sont constants jusqu’à environ nos 40 ans, puis nous devenons plus lents.
Exercice 2
Chargeons les données :
data(ChickWeight)
mypar()
plot(ChickWeight$Time, ChickWeight$weight, col=ChickWeight$Diet)
chick = reshape(ChickWeight, idvar=c("Chick","Diet"), timevar="Time",
direction="wide")
chick = na.omit(chick)Concentrez-vous sur les poids des poussins le jour 4 (vérifiez les noms de colonne du poussin et notez les chiffres). De combien la moyenne des poids des poussins au jour 4 augmente-t-elle si nous ajoutons une mesure aberrante de 3000 grammes ? Plus précisément, quel est le poids moyen des poussins du jour 4, y compris le poussin aberrant, divisé par la moyenne du poids des poussins du jour 4 sans la valeur aberrante. Astuce : utilisez c pour ajouter un nombre à un vecteur.
chick_w4 <- chick[,'weight.4']
chick_w4_add <- append(chick_w4, 3000)
# or use function c
# chick_w4_add <- c(chick_w4, 3000)
chick_w4_add ## [1] 59 58 55 56 48 59 57 59 52 63 56 53 62
## [14] 61 55 54 62 64 61 58 62 57 58 58 59 59
## [27] 62 65 63 63 64 61 56 61 61 66 66 63 69
## [40] 61 62 66 62 64 67 3000mean(chick_w4_add) - mean(chick_w4) # Difference between with and without outlier## [1] 63.90966mean(chick_w4_add)/mean(chick_w4) # Ratio between with and without outlier## [1] 2.062407Dans la première partie, nous avons vu à quel point la moyenne est sensible aux valeurs aberrantes. Voyons maintenant ce qui se passe lorsque nous utilisons la médiane au lieu de la moyenne. Calculez le même rapport, mais en utilisant maintenant la médiane au lieu de la moyenne. Plus précisément, quel est le poids médian des poussins du jour 4, y compris le poussin aberrant, divisé par la médiane du poids des poussins du jour 4 sans la valeur aberrante.
median(chick_w4_add) - median(chick_w4) # difference## [1] 0median(chick_w4_add)/median(chick_w4) # ratio## [1] 1Essayez maintenant la même chose avec l’exemple d’écart type (la fonction sd dans R). Ajoutez un poussin pesant 3000 grammes aux poids des poussins du jour 4. De combien l’écart type change-t-il ? Quel est l’écart type avec le poussin aberrant divisé par l’écart type sans le poussin aberrant ?
sd(chick_w4_add) - sd(chick_w4) # difference## [1] 429.1973sd(chick_w4_add)/ sd(chick_w4) # ratio## [1] 101.2859Comparez le résultat ci-dessus à l’écart absolu médian de R, qui est calculé avec la fonction mad. Notez que le mad n’est pas affecté par l’ajout d’une seule valeur aberrante. La fonction mad dans R inclut le facteur d’échelle 1,4826, de sorte que mad et sd sont très similaires pour un échantillon d’une distribution normale. Quel est le MAD avec le poussin aberrant divisé par le MAD sans le poussin aberrant ?
mad(chick_w4_add) - mad(chick_w4) # difference## [1] 0mad(chick_w4_add)/ mad(chick_w4) # ratio## [1] 1Notre dernière question porte sur la façon dont la corrélation de Pearson est affectée par une valeur aberrante par rapport à la corrélation de Spearman. La corrélation de Pearson entre x et y est donnée dans R par cor(x,y). La corrélation de Spearman est donnée par cor(x,y,method= »spearman »).
Tracez les poids des poussins du jour 4 et du jour 21. Nous pouvons voir qu’il existe une tendance générale, les poussins de poids inférieur le jour 4 ayant à nouveau un poids faible le jour 21, et de même pour les poussins de poids élevé.
Calculez la corrélation de Pearson des poids des poussins du jour 4 et du jour 21. Calculez maintenant de combien la corrélation de Pearson change si nous ajoutons un poussin qui pèse 3000 le jour 4 et 3000 le jour 21. Encore une fois, divisez la corrélation de Pearson avec la valeur aberrante chick sur la corrélation de Pearson calculée sans les valeurs aberrantes.
chick_w21 <- chick[, 'weight.21']
chick_w21## [1] 205 215 202 157 223 157 305 98 124 175 205 96 266 142 157 117
## [17] 331 167 175 74 265 251 192 233 309 150 256 305 147 341 373 220
## [33] 178 290 272 321 204 281 200 196 238 205 322 237 264plot(chick_w4, chick_w21)
cor(chick_w4,chick_w21) # correlation before## [1] 0.4159499chick_w21_add <- append(chick_w21, 3000)
cor(chick_w4_add, chick_w21_add) # correlation after outlier## [1] 0.9861002cor(chick_w4_add, chick_w21_add)/cor(chick_w4,chick_w21) # ratio between after and before## [1] 2.370719Enregistrez les poids des poussins au jour 4 du régime 1 en tant que vecteur x. Enregistrez les poids des poussins au jour 4 du régime 4 en tant que vecteur y. Effectuez un test t comparant x et y (dans R, la fonction t.test(x,y) effectuera le test). Effectuez ensuite un test de Wilcoxon de x et y (dans R, la fonction wilcox.test(x,y) effectuera le test). Un avertissement apparaîtra indiquant qu’une valeur p exacte ne peut pas être calculée avec des liens, donc une approximation est utilisée, ce qui est bien pour nos besoins.
Effectuez un test t de x et y, après avoir ajouté un seul poussin de 200 grammes à x (les poussins du régime 1). Quelle est la valeur p de ce test ? La valeur de p d’un test est disponible avec le code suivant : t.test(x,y)$p.value
x <- chick %>% filter(Diet == 1)
x <- x[,'weight.4']
y <- chick %>% filter(Diet == 4)
y <- y[,'weight.4']
t.test(x,y)$p.value # t.test result with no outlier## [1] 7.320259e-06wilcox.test(x,y)$p.value # wilcox result with no outlier## Warning in wilcox.test.default(x, y): cannot compute exact p-value
## with ties## [1] 0.0002011939x_add <- c(x,200) # outlier added
t.test(x_add,y)$p.value # t-test after outlier## [1] 0.9380347Faites de même pour le test de Wilcoxon. Le test de Wilcoxon est robuste à la valeur aberrante. De plus, il comporte moins d’hypothèses que le test t sur la distribution des données sous-jacentes.
wilcox.test(x_add,y)$p.value # even with outlier, p-value is not perturbed## Warning in wilcox.test.default(x_add, y): cannot compute exact p-
## value with ties## [1] 0.0009840921Nous allons maintenant étudier un éventuel inconvénient de la statistique du test de Wilcoxon-Mann-Whitney. En utilisant le code suivant pour créer trois boîtes à moustaches, montrant les vrais poids du régime 1 contre 4, puis deux versions modifiées : une avec une différence supplémentaire de 10 grammes et une avec une différence supplémentaire de 100 grammes. Utilisez les x et y tels que définis ci-dessus, PAS ceux avec la valeur aberrante ajoutée.
library(rafalib)
mypar(1,3)
boxplot(x,y)
boxplot(x,y+10)
boxplot(x,y+100)
Quelle est la différence dans la statistique du test t (obtenue par t.test(x,y)$statistic) entre l’ajout de 10 et l’ajout de 100 à toutes les valeurs du groupe y ? Prenez la statistique du test t avec x et y + 10 et soustrayez la statistique du test t avec x et y +100. La valeur doit être positive.
t.test(x,y+10)$statistic - t.test(x,y+100)$statistic ## t
## 67.75097Examinez la statistique du test de Wilcoxon pour x et y+10 et pour x et y+100. Étant donné que le Wilcoxon fonctionne sur les rangs, une fois que les deux groupes montrent une séparation complète, c’est-à-dire que tous les points du groupe y sont supérieurs à tous les points du groupe x, la statistique ne changera pas, quelle que soit l’ampleur de la différence. De même, la valeur p a une valeur minimale, quelle que soit la distance entre les groupes.
Cela signifie que le test de Wilcoxon peut être considéré comme moins puissant que le test t dans certains contextes. En fait, pour les petits échantillons, la valeur de p ne peut pas être très petite, même lorsque la différence est très grande. Quelle est la valeur de p si nous comparons c(1,2,3) à c(4,5,6) à l’aide d’un test de Wilcoxon ?
wilcox.test(x,y+10)$p.value## Warning in wilcox.test.default(x, y + 10): cannot compute exact p-
## value with ties## [1] 5.032073e-05wilcox.test(x,y+100)$p.value## Warning in wilcox.test.default(x, y + 100): cannot compute exact p-
## value with ties## [1] 5.032073e-05wilcox.test(c(1,2,3),c(4,5,6))$p.value # Answer## [1] 0.1Quelle est la valeur de p si nous comparons c(1,2,3) à c(400 500 600) à l’aide d’un test de Wilcoxon ?
wilcox.test(c(1,2,3),c(400,500,600))$p.value## [1] 0.1