Théorie des langages 101

Théorie des langages

En théorie des langages, l’ensemble des entités élémentaires est appelé l’alphabet. Une combinaison d’entités élémentaires est appelé un mot. Un ensemble de mots est appelé un langage et est décrit par une grammaire. A partir d’une grammaire, on peut construire une procédure effective (appelée automate) permettant de décider si un mot fait partie du langage.

Il existe différentes classes de langages, correspondant à différentes classes de grammaires et d’automates. Parmi les plus simple à étudier, la classe des langages réguliers correspond aux grammaires régulières et aux automates finis. Cette classe de grammaire est typiquement utilisée pour décrire de la domotique sans cycle.

Une classe plus globale que les langages réguliers est la classe des langages hors contexte, correspondant aux grammaires hors contexte et aux automates à pile. Cette classe de grammaire, plus puissante que la classe des grammaires régulières, est typiquement utilisée pour de la domotique ayant des cycles connus.

La théorie des langages est utile pour :

• décrire un comportement automatique (robotique, domotique, immotique)
• comprendre l’ensemble d’un langage et de ses utilités (compilateur, ADN, apprentissage automatique)
• Réduire au maximum un processus automatique (logiciel intégré, carte intégré pour l’aérospatial ou l’automobile etc.)

Alphabet

Un alphabet, noté A, est un ensemble fini non vide de symboles (lettres, signes, chiffres, etc.)

Un mot, défini sur un alphabet A, est une suite finie de symboles/éléments de A.

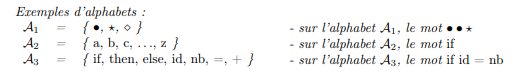
Quelques propriétés sur les mots:

• La longueur d’un mot u défini sur un alphabet A, notée |u| est le nombre de symboles (son cardinal) qui composent u.
• |u|_j compte le nombre d’occurrence du symbole j dans le mot u.
• Le mot vide, noté ε, est défini sur tous les alphabets et est le mot de longueur 0.
• L’ensemble de tous les mots formés à partir de l’alphabet A (resp. de tous les mots non vides) est noté A^* (resp. A⁺).
• La concaténation de deux mots u et v, notée, u.v ou uv, est le mot formé en faisant suivre les symboles de u par les symboles de v. Une puissance n d’un mot est ce mot concaténé n fois.
• si un ou des symboles est à la puissance + alors cela signifie qu’il existe un ou plus symbole de ce type dans le mot (ex. (ab)⁺=ab…)
• si un ou des symboles est à la puissance * alors cela signifie qu’il existe zéro ou plus symbole de ce type dans le mot

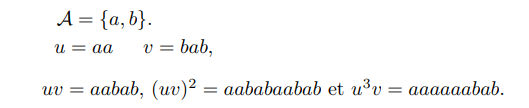
Soient deux mots u et v définis sur un alphabet A.

u est un préfixe de v si et seulement si il existe un mot (potentiellement vide) w tel que uw=v.

u est un suffixe de v si et seulement si il existe un mot (potentiellement vide) w tel que wu=v.

u est un facteur de v si et seulement si il existe deux mots (potentiellement vide) w₁ et w₂ tel que w₁uw₂=v.

un mot non-vide u est dit primitif si l’équation u=vⁱ n’admet pas de solution pour i>1.

deux mots x=uv et y=vu se déduisant l’un de l’autre par échange de préfixe et de suffixe sont dits conjugués.

Langages

Un langage, défini sur un alphabet A, est un ensemble de mots définis sur A. Un langage est un sous-ensemble de A^*.

Opérations ensemblistes définies sur les langages :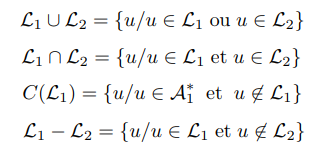

• L’union contient tous les mots qui sont soit contenus dans L₁ soit dans L₂.
• L’intersection est le langage qui contient tous les mots contenus à la fois dans L₁ et dans L₂.
• Le complément d’un langage est le langage contenant tous les mots qui ne sont pas dans ce langage.
• La différence entre deux langages est le langage contenant tous les mots de L₁ qui ne sont pas dans L₂.

Outre les opérations ensemblistes sur les langages, le produit ou concaténation de deux langages et défini par le langage contenant tous les mots formés de la concaténation d’un mot de L₁ suivi d’un mot de L₂. Le produit de langages est associatif mais non commutatif.

La puissance d’un langage est une concaténation successive de ce langage Lⁿ=L.L^n-1. La puissance 0 forme le langage composé du mot vide.

Considérons par exemple les deux langages L₁ = {00, 11} et L₂ = {0, 1, 01} définis sur {0,1}. L₁.L₂ = {000, 001, 0001, 110, 111, 1101}.

Grammaire

Un langage peut être décrit par un certain nombre de règles :  la grammaire indique comment construire des phrases appartenant au langage (fonctionnement en production) ; la grammaire permet également de décider si une phrase donnée appartient ou non au langage (fonctionnement en reconnaissance).

Une grammaire est un quadruplet G = (T, N, S, R) tel que:

• T est le vocabulaire terminal, c’est-à-dire l’alphabet sur lequel est défini le langage.
• N est le vocabulaire non terminal, c’est-à-dire l’ensemble des symboles qui n’apparaissent pas dans les mots générés, mais qui sont utilisés au cours de la génération. Un symbole non terminal désigne une catégorie syntaxique.
• R est un ensemble de règles dites de réécriture ou de production de la forme :     u1 → u2, avec u1 ∈ (N ∪ T)⁺ et u2 ∈ (N ∪ )^*. Rappelons que + signifie au moins un élément, et * signifie 0 ou plus. La signification intuitive de ces règles est que la suite non vide de symboles terminaux ou non terminaux u1 peut être remplacée par la suite éventuellement vide de symboles terminaux ou non terminaux u2.
• S ∈ N est le symbole de départ ou axiome. C’est à partir de ce symbole non terminal que l’on commencera la génération de mots au moyen des règles de la grammaire.

Lorsque plusieurs règles de grammaire ont une même forme en partie gauche, on
pourra factoriser ces différentes règles en séparant les parties droites par des traits verticaux. Par exemple, l’ensemble de règles S → ab, S → aSb, S → c pourra s’écrire S → ab | aSb | c.

Le langage défini, ou généré, par une grammaire est l’ensemble des mots qui peuvent être obtenus à partir du symbole de départ par application des règles de la grammaire. Plus formellement, on introduit les notions de dérivation entre formes, cela consiste à remplacer un symbole non terminal par une suite de symbole terminaux et non-terminaux suivant les règles de grammaire.

Pour des compléments d’informations sur les opérations entre langage et grammaire merci de se référencer à la table des liens en haut de ce cours.