Maintenant, supposons que vous ayez choisi le meilleur modèle possible pour un problème particulier et que vous vous efforciez d’améliorer encore sa précision. Dans ce cas, vous devrez appliquer des techniques d’apprentissage automatique plus avancées qui sont collectivement appelées apprentissage d’ensembles.
Un ensemble est un ensemble d’éléments qui contribuent collectivement à un tout. Un exemple familier est un ensemble musical, qui mélange les sons de plusieurs instruments de musique pour créer une belle harmonie, ou des ensembles architecturaux, qui sont un ensemble de bâtiments conçus comme une unité. Dans les ensembles, le (tout) résultat harmonieux est plus important que l’exécution de n’importe quelle partie individuelle.
Le théorème du jury de Condorcet (1784) concerne un ensemble dans un certain sens. Il stipule que, si chaque membre du jury rend un jugement indépendant et que la probabilité de la décision correcte de chaque juré est supérieure à 0,5, alors la probabilité de la décision correcte de l’ensemble du jury augmente avec le nombre total de jurés et tend à une. En revanche, si la probabilité d’avoir raison est inférieure à 0,5 pour chaque juré, alors la probabilité d’une décision correcte par l’ensemble du jury décroît avec le nombre de jurés et tend vers zéro.
Prenons un autre exemple d’ensembles : une observation connue sous le nom de Sagesse de la foule. En 1906, Francis Galton a visité une foire rurale à Plymouth où il a vu un concours organisé pour les agriculteurs. 800 participants ont tenté d’estimer le poids d’un taureau abattu. Le poids réel du taureau était de 1198 livres. Bien qu’aucun des agriculteurs ne puisse deviner le poids exact de l’animal, la moyenne de leurs prévisions était de 1197 livres.
Une idée similaire pour la réduction des erreurs a été adoptée dans le domaine de l’apprentissage automatique.
Amorçage (bagging et bootstraping)
Le bagging (également connu sous le nom d’agrégation Bootstrap) est l’une des premières et des plus basiques techniques d’ensemble. Il a été proposé par Leo Breiman en 1994. Le bagging est basé sur la méthode statistique du bootstrap, qui rend possible l’évaluation de nombreuses statistiques de modèles complexes.
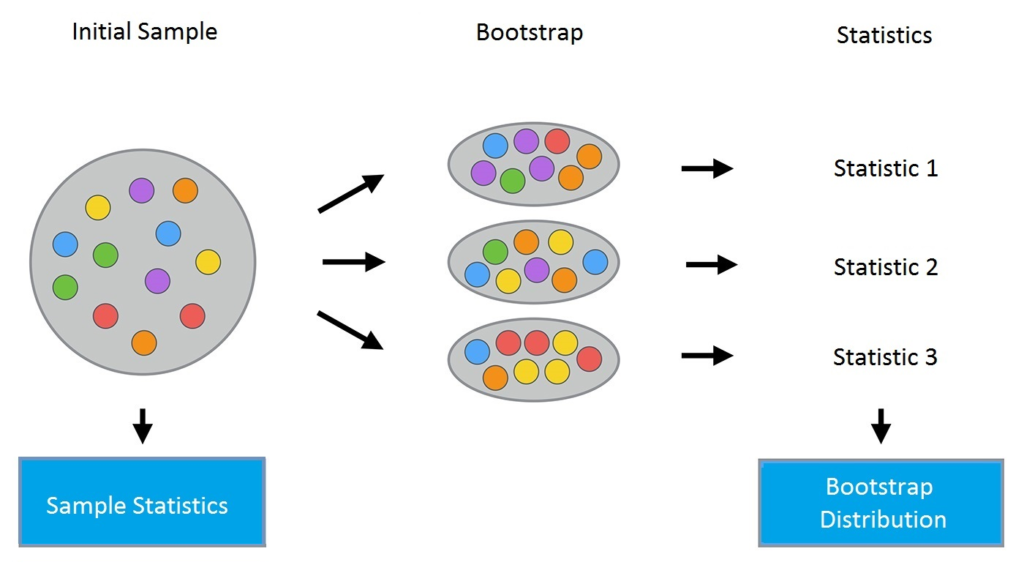
La méthode bootstrap se déroule comme suit. Soit un échantillon X de taille N. On peut faire un nouvel échantillon à partir de l’échantillon original en tirant N éléments de ce dernier de façon aléatoire et uniforme, avec remise. En d’autres termes, nous sélectionnons un élément aléatoire dans l’échantillon original de taille N et le faisons N fois. Tous les éléments sont également susceptibles d’être sélectionnés, ainsi chaque élément est tiré avec la probabilité égale 1/N.
Disons que nous tirons des boules d’un sac une à la fois. A chaque étape, la bille sélectionnée est remise dans le sac pour que la sélection suivante se fasse de manière équiprobable c’est-à-dire à partir du même nombre de billes N. A noter que, du fait qu’on remet les billes, il peut y avoir des doublons dans le nouvel échantillon. Appelons ce nouvel échantillon X1.
En répétant cette procédure M fois, on crée M échantillons bootstrap X1, …, XM. En fin de compte, nous avons un nombre suffisant d’échantillons et pouvons calculer diverses statistiques de la distribution d’origine.
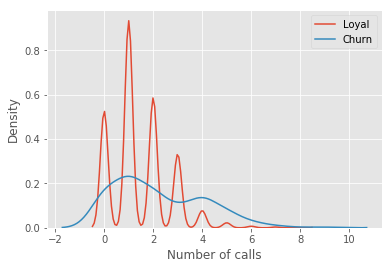
Pour notre exemple, nous utiliserons le jeu de données familier telecom_churn. Auparavant, lorsque nous avons discuté de l’importance des fonctionnalités, nous avons vu que l’une des fonctionnalités les plus importantes de cet ensemble de données est le nombre d’appels au service client. Visualisons les données et regardons la distribution de cette fonctionnalité.
| import pandas as pd | |
| from matplotlib import pyplot as plt | |
| plt.style.use(‘ggplot’) | |
| plt.rcParams[‘figure.figsize’] = 10, 6 | |
| import seaborn as sns | |
| %matplotlib inline | |
| telecom_data = pd.read_csv(‘../../data/telecom_churn.csv’) | |
| fig = sns.kdeplot(telecom_data[telecom_data[‘Churn’] == False][‘Customer service calls’], | |
| label = ‘Loyal’) | |
| fig = sns.kdeplot(telecom_data[telecom_data[‘Churn’] == True][‘Customer service calls’], | |
| label = ‘Churn’) | |
| fig.set(xlabel=‘Number of calls’, ylabel=‘Density’) | |
| plt.show() |
| import numpy as np | |
| def get_bootstrap_samples(data, n_samples): | |
| « » »Generate bootstrap samples using the bootstrap method. » » » | |
| indices = np.random.randint(0, len(data), (n_samples, len(data))) | |
| samples = data[indices] | |
| return samples | |
| def stat_intervals(stat, alpha): | |
| « » »Produce an interval estimate. » » » | |
| boundaries = np.percentile(stat, [100 * alpha / 2., 100 * (1 – alpha / 2.)]) | |
| return boundaries | |
| # Save the data about the loyal and former customers to split the dataset | |
| loyal_calls = telecom_data[telecom_data[‘Churn’] | |
| == False][‘Customer service calls’].values | |
| churn_calls= telecom_data[telecom_data[‘Churn’] | |
| == True][‘Customer service calls’].values | |
| # Set the seed for reproducibility of the results | |
| np.random.seed(0) | |
| # Generate the samples using bootstrapping and calculate the mean for each of them | |
| loyal_mean_scores = [np.mean(sample) | |
| for sample in get_bootstrap_samples(loyal_calls, 1000)] | |
| churn_mean_scores = [np.mean(sample) | |
| for sample in get_bootstrap_samples(churn_calls, 1000)] | |
| # Print the resulting interval estimates | |
| print(« Service calls from loyal: mean interval », | |
| stat_intervals(loyal_mean_scores, 0.05)) | |
| print(« Service calls from churn: mean interval », | |
| stat_intervals(churn_mean_scores, 0.05)) |
Bagging
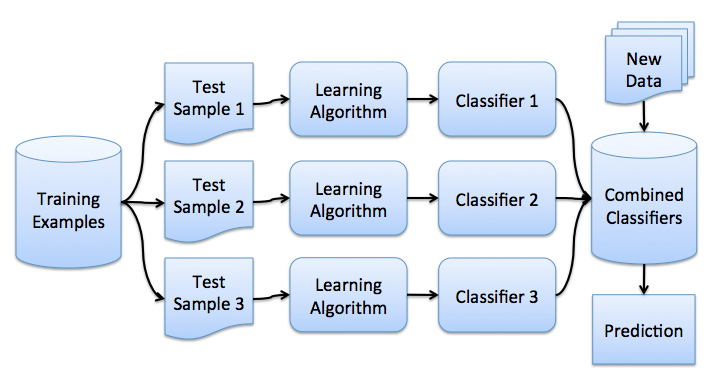
Maintenant que vous avez saisi l’idée du bootstrap, nous pouvons passer au bagging. Dans un problème de régression, en faisant la moyenne des réponses individuelles, le bagging réduit l’erreur quadratique moyenne d’un facteur M, le nombre de régresseurs.
De notre leçon précédente, rappelons les composants qui composent l’erreur totale hors échantillon :
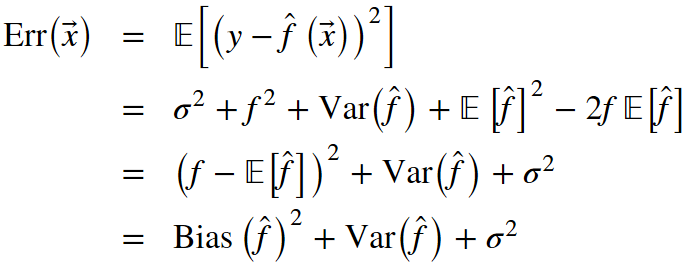
Le bagging réduit la variance d’un classificateur en diminuant la différence d’erreur lorsque nous entraînons le modèle sur différents ensembles de données. En d’autres termes, le bagging empêche le surajustement. L’efficacité du bagging vient du fait que les modèles individuels sont assez différents en raison des différentes données d’entraînement et que leurs erreurs s’annulent lors du vote. De plus, les valeurs aberrantes sont probablement omises dans certains des échantillons de démarrage de formation.
La bibliothèque scikit-learn prend en charge le bagging avec les méta-estimateurs BaggingRegressor et BaggingClassifier. Vous pouvez utiliser la plupart des algorithmes comme base.
Examinons comment fonctionne le bagging dans la pratique et comparons-le avec l’arbre de décision. Pour cela, nous utiliserons un exemple de la documentation de sklearn.
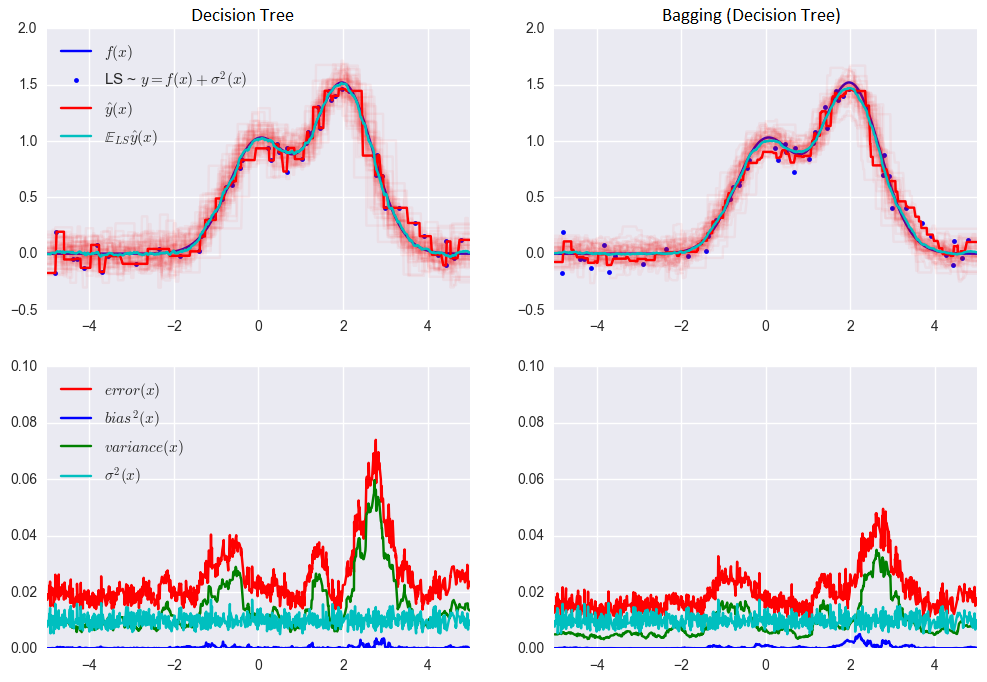
L’erreur pour l’arbre de décision :
0,0255 = 0,0003 (biais²)+ 0,0152 (variance) + 0,0098 (σ²)
L’erreur lors de l’utilisation de l’ensachage :
0,0196 = 0,0004 (biais²) + 0,0092 (variance) + 0,0098 (σ²)
Comme vous pouvez le voir sur le graphique ci-dessus, la variance de l’erreur est beaucoup plus faible pour l’ensachage. Rappelez-vous que nous avons déjà prouvé cela théoriquement.
Le bagging est efficace sur les petits ensembles de données. La suppression même d’une petite partie des données d’apprentissage conduit à la construction de classificateurs de base sensiblement différents. Si vous disposez d’un grand ensemble de données, vous générerez des échantillons bootstrap d’une taille beaucoup plus petite.
Il est peu probable que l’exemple ci-dessus s’applique à un travail réel. C’est parce que nous avons fait l’hypothèse forte que nos erreurs individuelles ne sont pas corrélées. Le plus souvent, c’est beaucoup trop optimiste pour les applications du monde réel. Lorsque cette hypothèse est fausse, la réduction de l’erreur ne sera pas aussi importante. Dans les conférences suivantes, nous discuterons de certaines méthodes d’ensemble plus sophistiquées, qui permettent des prédictions plus précises dans des problèmes du monde réel.
Erreur hors sac (out-of-bag error)
À l’avenir, dans le cas d’une forêt aléatoire, il n’est pas nécessaire d’utiliser des échantillons de validation croisée ou d’exclusion pour obtenir une estimation d’erreur impartiale. Pourquoi? Parce que, dans les techniques d’ensemble, l’estimation de l’erreur a lieu en interne.
Des arbres aléatoires sont construits à l’aide de différents échantillons bootstrap de l’ensemble de données d’origine. Environ 37 % des entrées sont exclues d’un échantillon bootstrap particulier et ne sont pas utilisées dans la construction du K-ième arbre.
Voyons comment fonctionne l’estimation de l’erreur Out-of-Bag (ou OOBE) :
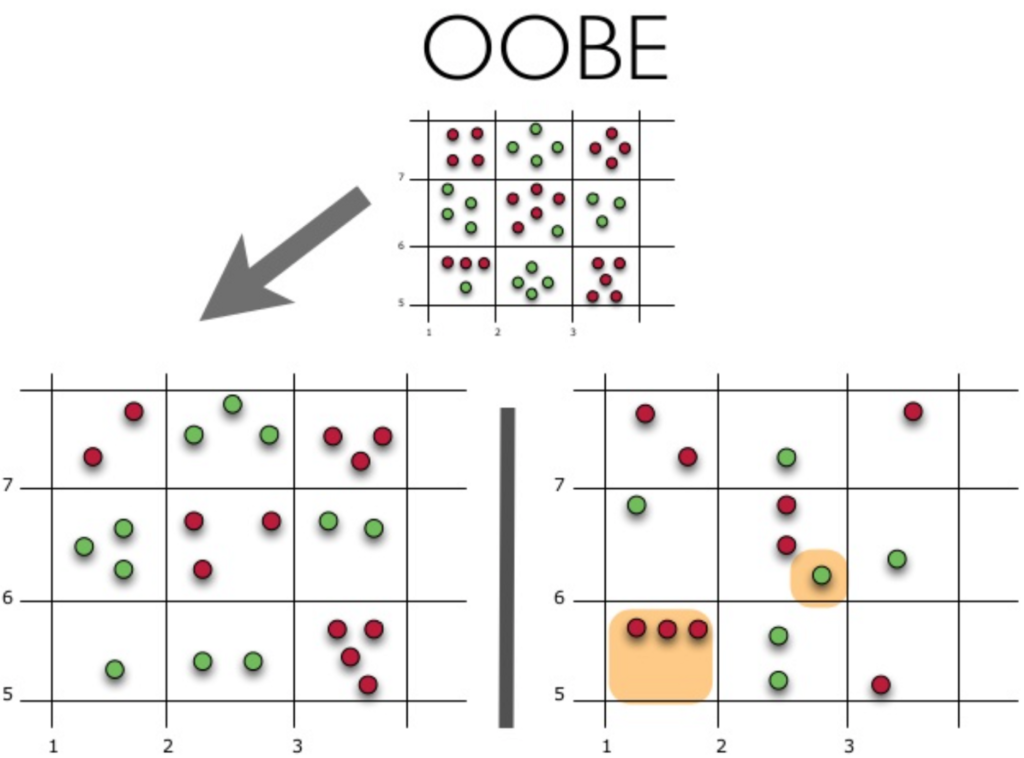
La partie supérieure de la figure ci-dessus représente notre ensemble de données d’origine. Nous l’avons divisé en ensembles d’entraînement (à gauche) et de test (à droite). Dans l’image de gauche, nous dessinons une grille qui divise parfaitement notre jeu de données selon les classes. Maintenant, nous utilisons la même grille pour estimer la part des bonnes réponses sur notre ensemble de test. Nous pouvons voir que notre classificateur a donné des réponses incorrectes dans ces 4 cas qui n’ont pas été utilisés pendant la formation (à gauche). Par conséquent, la précision de notre classificateur est de 11/15*100 % = 73,33 %.
Pour résumer, chaque algorithme de base est entraîné sur ~ 63 % des exemples originaux. Il peut être validé sur les ~37% restants. L’estimation Out-of-Bag n’est rien de plus que l’estimation moyenne des algorithmes de base sur les ~37 % d’entrées qui n’ont pas été entraînées.
Forêt aléatoire (Random forest)
Leo Breiman a réussi à appliquer le bootstrap non seulement dans les statistiques mais aussi dans l’apprentissage automatique. Avec Adel Cutler, il a étendu et amélioré l’algorithme Random Forest proposé par Tin Kam Ho. Ils ont combiné la construction d’arbres non corrélés à l’aide de CART, de bagging et de la méthode du sous-espace aléatoire.
Les arbres de décision sont un bon choix pour le classificateur de base dans l’ensachage car ils sont assez sophistiqués et peuvent atteindre zéro erreur de classification sur n’importe quel échantillon. La méthode du sous-espace aléatoire réduit la corrélation entre les arbres et évite ainsi le surajustement. Avec le bagging, les algorithmes de base sont formés sur différents sous-ensembles aléatoires de l’ensemble de fonctionnalités d’origine.
L’algorithme suivant construit un ensemble de modèles en utilisant la méthode du sous-espace aléatoire :
- Supposons que le nombre d’instances soit égal à n et que le nombre de dimensions de l’entité soit égal à d.
- Choisissez M comme nombre de modèles individuels dans l’ensemble.
- Pour chaque modèle m, choisissez le nombre de caractéristiques dm < d. En règle générale, la même valeur de dm est utilisée pour tous les modèles.
- Pour chaque modèle m, créez un ensemble d’apprentissage en sélectionnant dm caractéristiques au hasard parmi l’ensemble des caractéristiques d.
- Entraînez chaque modèle.
- Appliquez le modèle d’ensemble résultant à une nouvelle entrée en combinant les résultats de tous les modèles de M. Vous pouvez utiliser soit le vote à la majorité, soit l’agrégation des probabilités postérieures.
L’algorithme est le suivant :
Le classifieur final est la moyenne des arbres.
Pour les problèmes de classification, il est conseillé de fixer m égal à la racine carrée de d. Pour les problèmes de régression, nous prenons généralement m = d/3, où d est le nombre de caractéristiques. Il est recommandé de construire chaque arbre jusqu’à ce que toutes ses feuilles contiennent seulement 1 instance pour la classification et 5 instances pour la régression.
Vous pouvez voir Random Forest comme un regroupement d’arbres de décision avec la modification de la sélection d’un sous-ensemble aléatoire de fonctionnalités à chaque fractionnement.
Comparaison
Voici les résultats pour les trois algorithmes :
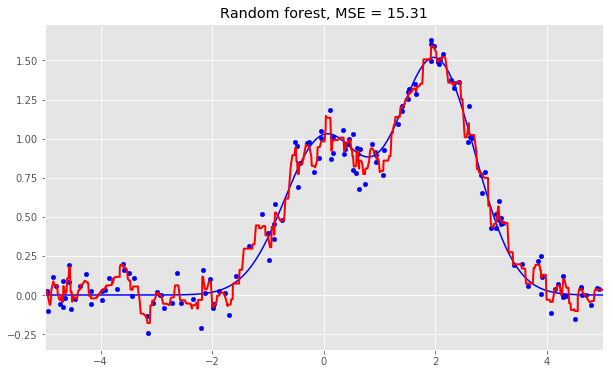
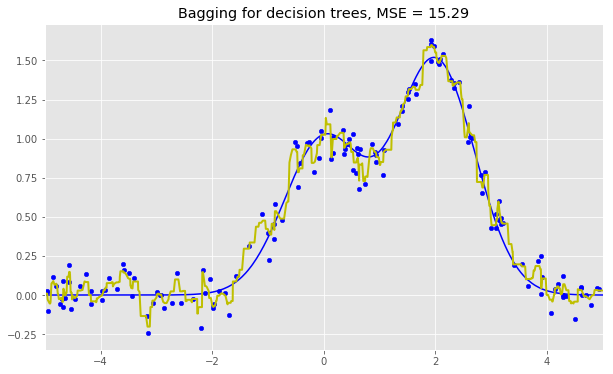
As we can see from our graphs and the MSE values above, a Random Forest of 10 trees achieves a better result than a single decision tree and is comparable to bagging with 10 trees. The main difference between Random Forests and bagging is that, in a Random Forest, the best feature for a split is selected from a random subset of the available features while, in bagging, all features are considered for the next best split.
Nous pouvons également examiner les avantages des forêts aléatoires et des problèmes de classification.
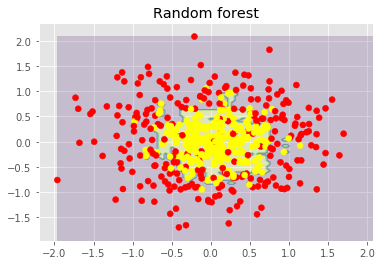
Les figures ci-dessus montrent que la frontière de décision de l’arbre de décision est assez irrégulière et présente de nombreux angles aigus qui suggèrent un surajustement et une faible capacité à généraliser. Nous aurions du mal à faire des prédictions fiables sur de nouvelles données de test. En revanche, l’algorithme de bagging a une frontière plutôt lisse et ne présente aucun signe évident de surajustement.
Examinons maintenant certains paramètres qui peuvent nous aider à augmenter la précision du modèle.
Paramètres pour augmenter la précision
La bibliothèque scikit-learn implémente des forêts aléatoires en fournissant deux estimateurs : RandomForestClassifier et RandomForestRegressor.
Vous trouverez ci-dessous les paramètres auxquels nous devons prêter attention lorsque nous construisons un nouveau modèle :
- n_estimators est le nombre d’arbres dans la forêt ;
- critère est la fonction utilisée pour mesurer la qualité d’un fractionnement ;
- max_features est le nombre de fonctionnalités à prendre en compte lors de la recherche de la meilleure répartition ;
- min_samples_leaf est le nombre minimum d’échantillons requis pour être à un nœud feuille ;
- max_depth est la profondeur maximale de l’arbre.
Le fait le plus important à propos des forêts aléatoires est que sa précision ne diminue pas lorsque nous ajoutons des arbres, de sorte que le nombre d’arbres n’est pas un hyperparamètre de complexité contrairement à max_depth et min_samples_leaf. Cela signifie que vous pouvez ajuster les hyperparamètres avec, disons, 10 arbres, puis augmenter le nombre d’arbres jusqu’à 500 et être sûr que la précision ne fera que s’améliorer.
Les arbres extrêmement aléatoires utilisent un plus grand degré de randomisation au choix du point de coupure lors de la division d’un nœud d’arbre. Comme dans Random Forests, un sous-ensemble aléatoire d’entités est utilisé. Mais, au lieu de rechercher des seuils optimaux, leurs valeurs sont sélectionnées au hasard pour chaque caractéristique possible, et le meilleur parmi ces seuils générés aléatoirement est utilisé comme meilleure règle pour diviser le nœud. Cela compense généralement une légère réduction de la variance du modèle par une légère augmentation du biais.
Dans la bibliothèque scikit-learn, il existe 2 implémentations d’arbres extrêmement aléatoires : ExtraTreesClassifier et ExtraTreesRegressor.
Cette méthode doit être utilisée si vous avez largement surfait avec les forêts aléatoires ou l’amplification de gradient.
Conclusion sur le random forest
Avantages:
- Haute précision de prédiction ; fonctionnera mieux que les algorithmes linéaires dans la plupart des problèmes ; la précision est comparable à celle du boosting ;
- Robuste aux valeurs aberrantes, grâce à un échantillonnage aléatoire ;
- Insensible à la mise à l’échelle des caractéristiques ainsi qu’à toute autre transformation monotone en raison de la sélection aléatoire du sous-espace ;
- Ne nécessite pas de réglage fin des paramètres, fonctionne assez bien prêt à l’emploi. Avec le réglage, il est possible d’obtenir un gain de précision de 0,5 à 3 %, en fonction du réglage du problème et des données ;
- Efficace pour les jeux de données avec un grand nombre d’entités et de classes ;
- Gère aussi bien les variables continues que discrètes ;
- Rarement surdimensionné. En pratique, une augmentation du nombre d’arbres améliore presque toujours la composition. Mais, après avoir atteint un certain nombre d’arbres, la courbe d’apprentissage est très proche de l’asymptote ;
- Il existe des méthodes développées pour estimer l’importance des caractéristiques;
- Fonctionne bien avec les données manquantes et maintient de bons niveaux de précision même lorsqu’une grande partie des données est manquante ;
- Fournit des moyens de pondérer les classes sur l’ensemble de données ainsi que pour chaque échantillon d’arbre ;
- Sous le capot, calcule les proximités entre les paires d’instances qui peuvent ensuite être utilisées dans le regroupement, la détection des valeurs aberrantes ou des représentations de données intéressantes ;
- La fonctionnalité et les propriétés ci-dessus peuvent être étendues aux données non étiquetées pour permettre un regroupement non supervisé, la visualisation des données et la détection des valeurs aberrantes ;
- Facilement parallélisé et hautement évolutif.
Les inconvénients:
- En comparaison avec un arbre de décision unique, la sortie de Random Forest est plus difficile à interpréter.
- Il n’y a pas de valeurs de p formelles pour l’estimation de l’importance des caractéristiques.
- Effectue moins bien que les méthodes linéaires dans le cas de données éparses : saisies de texte, sac de mots, etc. ;
- Contrairement à la régression linéaire, Random Forest est incapable d’extrapoler. Mais cela peut également être considéré comme un avantage car les valeurs aberrantes ne provoquent pas de valeurs extrêmes dans les forêts aléatoires ;
- Enclin au surajustement dans certains problèmes, en particulier lorsqu’il s’agit de données bruyantes ;
- Dans le cas de variables catégorielles avec des nombres de niveaux variables, les forêts aléatoires favorisent les variables avec un plus grand nombre de niveaux. L’arborescence s’adaptera davantage à une fonctionnalité à plusieurs niveaux, car cela gagne en précision ;
- Si un jeu de données contient des groupes d’entités corrélées avec une importance similaire pour les classes prédites, la préférence sera donnée aux groupes plus petits ;
- Le modèle résultant est volumineux et nécessite beaucoup de RAM.
FR 
EN 
ES