Contents
ToggleDistance measurements for attributes of mixed type
Many methods of partitioning use distance measures to determine the similarity or dissimilarity between any pair of objects (like Distance Measures for attributes of mixed type). It is common to denote the distance between two instances x_i and x_j as: d(x_i, x_j). A valid distance measure must be symmetric and obtains its minimum value (usually zero) in the case of identical vectors. The distance measure is called a metric distance measure if it also satisfies the following properties:

In cases where the instances are characterized by attributes of mixed type, one can calculate the distance by combining different methods. For example, when calculating the distance between instances i and j using a metric such as Euclidean distance, one can calculate the difference between the nominal attributes and binary as 0s or 1s (“match” or “mismatch”, respectively), and the difference between the numeric attributes as the difference between their normalized values. The square of each of these differences will be added to the total distance. Such a calculation is used in many clustering algorithms.
The dissimilarity d (x_i, x_j) between two instances, containing p attributes of mixed types, is defined as:

where the indicator δ = 0 if one of the values is missing. The contribution of attribute n to the distance between the two objects d ^ (n) is calculated according to its type.
If the attribute is binary or categorical:
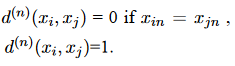
If the attribute has a continuous value (where h goes through all non-missing objects for attribute n):
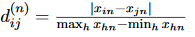
If the attribute is ordinal, the normalized values of the attribute are first calculated, then z_i, n is treated as a continuous value.
