Contents
ToggleExternal quality criteria
External quality indices are indices intended to measure the similarity between two partitions. They only take into account the distribution of points in the different clusters and do not make it possible to measure the quality of this distribution.

List
- Precision recall measurement
- Indicator variables
- Measure based on mutual information
- Entropy, purity and V-measure
- Czekanowski-Dice
- Folkes-Mallows
- Hubert Γ
- Jaccard
- Kulczynski
- McNemar
- Phi
- Rand
- Rogers-Tanimoto
- Russell Rao
- Sokal-Sneath
Rating
All the proposed indices are based on a confusion matrix representing the counting of pairs of points depending on whether or not they are considered to belong to the same cluster according to partition P1 or partition P2. There are therefore four possibilities:
• the two points belong to the same cluster, according to P1 and P2
• the two points belong to the same cluster according to P1 but not to P2
• the two points belong to the same cluster according to P2 but not to P1
• the two points do not belong to the same cluster, according to P1 and P2.
Let us note yy, yn, ny, nn (y means yes, and n means no) the number of points belonging respectively to these four categories. NT being the total number of pairs of points, we have:
![]()
Precision recall measurement and F-measure
If the partition P1 is used as a reference, we define the precision coefficient as the proportion of points precisely grouped in P2, that is to say which are also grouped according to the reference partition P1. Among the points yy + ny grouped according to P2, yy are rightly grouped. So we have :
![]()
Likewise, we define the recall coefficient as the proportion of points grouped in P1 which are also grouped in the partition P2. This is the proportion of points which are supposed to be grouped according to the reference partition P1 and which are actually identified as such by the partition P2. Among the points yy+yn grouped in P1, yy are also grouped in P2. So we have :
![]()
In terms of conditional probabilities, we can write
![]()
where the events gp1 and gp2 mean that two points are grouped into P1 and P2 respectively.
The F measure is the harmonic average of the precision and recall coefficients:

There is also a weighted version of this measure, called the Fα measure, defined as follows:
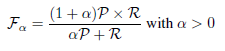
Indicator variables
Let us associate with each partition Pa (a = 1, 2) the binary random variable Xa defined on the set of indices i and j such that i < j as follows: its value is 1 if the points Mi and Mj are classified in the same cluster only in partition Pa and 0 otherwise. The variable Xa functions as an indicator variable.
There exist NT pairs of points and we are only interested in the indices i and j such that i < j. Consider the mean and standard deviation of Xa:
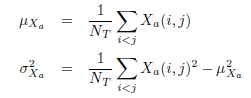
The following formulas relate these random variables to the matching and discordant count variables:

From here we get:

Measure based on mutual information
The mutual information criterion can be used as an external measure for clustering. The measure for m instances grouped together using C = {C_1 ,. . . , C_g} and referring to the target attribute y whose domain is dom (y) = {c_1 ,. . . , c_k} is defined as follows:
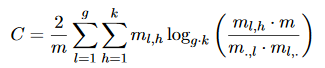
where m_l, h indicates the number of instances that are in cluster C_l and also in class c_h. m., h indicates the total number of instances in class c_h. Likewise, m_l ,. indicates the number of instances of the C_l cluster.
MI is combined with entropy in the NMI:

MI is combined with entropy in AMI:
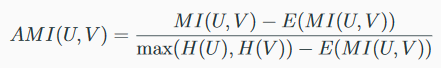
Entropy, purity and V-measure
Since the complete cluster (all objects of a same class are assigned to a single cluster) and the homogeneous cluster (each cluster contains only objects of a same class) are rarely achieved, we aim to achieve an equilibrium satisfactory between these two approaches. Therefore, we generally apply five well-known clustering criteria in order to evaluate partition performance, which are purity, H-entropy, V-metric, RAND index, and F-metric. This page exposes the three first. The others are exposed in another page.
The entropy measure is used to show how sentence clusters are partitioned within each cluster, and it is known as the average of the weighted values in each cluster entropy over all clusters C = {c_1, …, c_n} :

The purity of a cluster is the fraction of the size of the cluster represented by the largest class of sentences assigned to this cluster, namely:
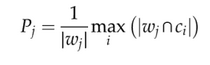
The overall purity is the weighted sum of the purities of the individual clusters given by:
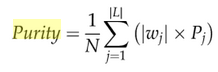
Although purity and entropy are useful for comparing partitioning with the same number of clusters, they are not reliable when comparing partitioning with different numbers of clusters. This is because entropy and purity operate on how sets of sentences are partitioned within each cluster, and this will lead to a case of homogeneity. The highest purity scores and lowest entropy scores are usually obtained when the total number of clusters is too large, where this step will lead to being the lowest in completeness. The next measure considers both the completeness and homogeneity approaches.
The V measure is known as the harmonic mean of homogeneity and completeness; that is, V = homogeneity * completeness / (homogeneity + completeness), where homogeneity and completeness are defined as homogeneity = 1-H (C | L) / H (C) and completeness = 1-H (L | C) / H (L) where:

Czekanowski-Dice
The Czekanowski-Dice index (aka the Ochiai index) is defined like this:
![]()
This index is the harmonic average of the precision and recall coefficients, that is to say it is identical to the F-measure:
![]()
Folkes-Mallows
The Folkes-Mallows index is defined as follows:
![]()
This index is the geometric mean (square root of the multiplication) of the precision and recall coefficients.
Hubert Γ
The Hubert index ˆΓ is the coefficient of correlation indicator variables. It is defined as follows:
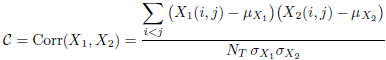
The Hubert index ˆΓ appears as a standardized variant (centered and reduced) of the Russell-Rao index. Its value is between -1 and 1. We can write the index ˆΓ as follows:
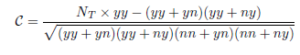
Jaccard
The Jaccard index is defined as follows:
![]()
Kulczynski
The Kulczynski index is defined as follows:
![]()
This index is the arithmetic average of the precision and recall coefficients.
McNemar
The McNemar index is defined as follows:
![]()
Under the null hypothesis H0 that the mismatches between partitions P1 and P2 are random, the index C approximately follows a normal distribution. This is an adaptation of the non-parametric McNemar test for comparing frequencies between two paired samples: the McNemar test statistic (called χ2 distance) is the square of the index:
![]()
and follows, under the null hypothesis of marginal homogeneity of the contingency table, a Chi-square distribution with 1 degree of freedom.
Phi
The Phi index is a classic measure of the correlation between two dichotomous variables. It is defined as follows:
![]()
Rand
The Rand index is a simple criterion used to compare an induced aggregation structure (C1) with a given aggregation structure (C2). Let a be the number of pairs of instances assigned to the same cluster in C1 and in the same cluster in C2; let b be the number of pairs of instances which are in the same cluster C1, but not in the same cluster C2; let c be the number of pairs of instances which are in the same cluster C2, but not in the same cluster C1; and d the number of pairs of instances allocated to different clusters than C1 and C2.
The quantities a and d can be interpreted as agreements, and b and c as disagreements. The Rand index is defined as:
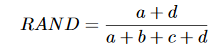
What comes down with the rating system is
(yy+nn)/NT
The Rand index is between 0 and 1. When the two partitions match perfectly, the Rand index is 1.
One problem with the Rand index is that its expected value of two random groupings does not take a constant value (such as zero). Hubert and Arabia in 1985 suggest an adjusted Rand index which overcomes this drawback.
Rogers-Tanimoto
The Rogers-Tanimoto index is defined as follows:
![]()
Russell Rao
The Russell-Rao index measures the proportion of matches between the two partitions. It is defined as follows:
![]()
This index can also be written:
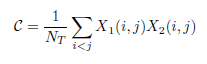
Sokal-Sneath
There are two versions of the Sokal-Sneath index. They are defined respectively as follows:

