Contents
ToggleOut-of-kilter algorithm
Also called algorithm of Fulkerson-Ford (not to be confused with the algorithm of maximum flow), the out-of-kilter algorithm calculates a maximum flow at minimum cost with min and max bounds on the edges.
We will say that an edge is In-Kilter if it satisfies the additional deviations, otherwise we'll say it's Out-of-Kilter (kilter means "in good condition").
The following explanations will not be translated for the sake of understanding the underlying logic in the sense of "kilter".
Theorem: A feasible solution x * is an optimal solution of the MCF problem if and only if for some set of node potentials π, the reduced costs and flow values satisfy the following complementary slackness conditions for every edge (u, v) in the network:
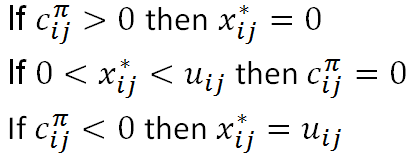
Which gives the following efficiency diagram:

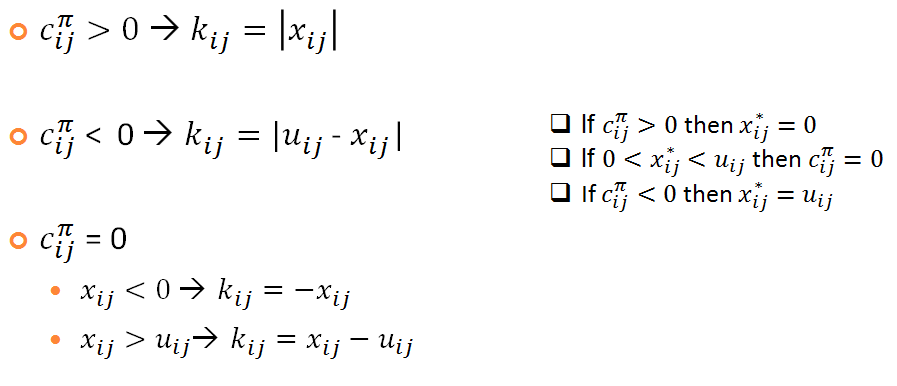


Correctness:
- Kilter numbers of the edges are non-increasing
- Two operations in the algorithm affect the kilter numbers of arcs:
- updating node potentials
- augmenting flow along the cycle W
- At each iteration the algorithm selects and edge (p, q)
- Makes it in-kilter during potential update
- decrease it by at least 1 by the flow increase
- Two operations in the algorithm affect the kilter numbers of arcs:
The algorithm terminate within O (mU) iterations, total runtime is: O (m ^ 2 U + mUn log n)
