Poisson process

Poisson process

A Poisson process with parameter λ is a stochastic process N (t) such that N (O) = 0, N (t) is incremented by +1 after a time T distributed according to an exponential law with parameter λ. We speak of Poisson arrivals if the time between two arrivals is exponential.

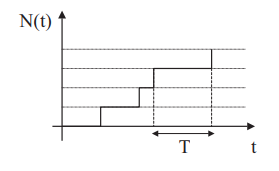
Take as state the value of N(t), then the markov chain in continuous time associated with the Poisson process λ is:

It is possible to know the probability that N is number k at time t by the formula:

N (t) is distributed according to a Poisson law with parameter λt.

The Poisson processes associate and decompose as follows:

• The superposition of n Poisson process is a Poisson process having for parameter the sum of the n parameters
• A Poisson process which decomposes into n processes with probabilities pi. These n processes are then Poisson processes with respective rates λp_i