Contenus
ToggleExercices corrigés sur le programme dual et écart complémentaire
Ce TD propose divers exercices corrigés sur le programme dual et l’algorithme d’écart complémentaire. Les exercices sont suivis des corrections.

Tutoriel
Prenons le programme linéaire suivant :
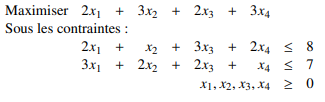
Résoudre le programme linéaire.
Il y a quatre variables de base pour deux contraintes, il est possible que le problème ne soit pas borné et ne possède pas de solution. Puisqu’il y a deux contraintes, le dual aura deux variables, il est facile de trouver une solution graphique à ce nouveau programme linéaire.
Le dual est le suivant :

Et voici sa représentation graphique, avec un minimum en (1,1) et pour fonction objectif 15.
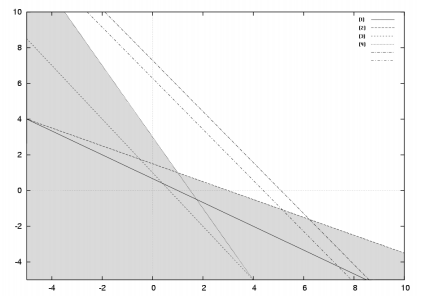
Regardons les écarts complémentaires pour trouver une solution du primal.
- Les deux variables sont non-nulles, donc les deux contraintes du primal sont saturés (la contraintes devient égalité).
- Dans le dual, les contraintes 1 et 3 sont non saturés pour la solution (1,1), cela signifie que la première variable et la troisième variable du primal sont nulles.
Nous avons donc les deux équations suivantes à résoudre :
- x2 + 2x4 = 8
- 2x2 + x4 = 7
Ce qui donne pour solution (0, 2, 0, 3) et pour fonction objectif 15. Les solutions du primal et dual sont égales, il y a dualité forte, il s’agit donc d’une solution optimale.
Exercice 1
Résoudre le programme linéaire suivant à l’aide du dual (résolution graphique + simplexe et écarts complémentaires) :
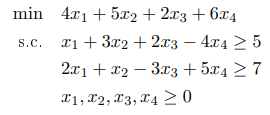
Le programme linéaire est sous forme canonique, on peut donc calculer le dual sans changer la forme du programme. Le dual est le suivant :

avec pour résolution graphique :
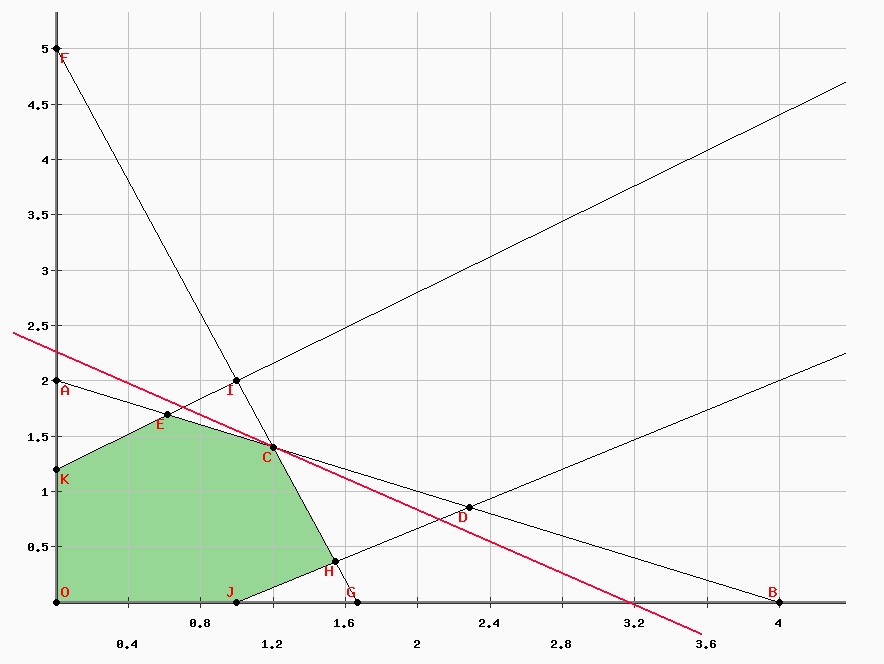
L’optimum global est unique est se situe au point (6/5, 7/5) avec pour fonction objectif Z= 79/5.
Pour le simplexe, la forme standard rajoute une variable d’écart pour chaque contrainte du programme linéaire. Le tableau final est :
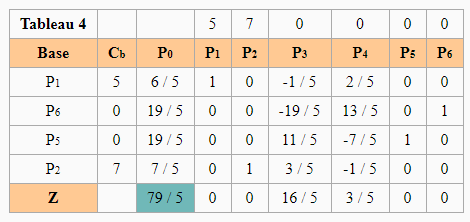
Le vecteur de solution du dual est (6/5, 7/5, 0, 0, 19/5, 19/5) avec Z=79/5. Les écarts complémentaires donnent les informations suivantes :
- La troisième et quatrième contraintes du dual sont non saturés, la troisième et quatrième variables du primal sont nulles.
- Les deux variables de base sont non nulles, les deux contraintes du primal sont donc saturées.
Il faut donc résoudre le système d’équations :
- x1 + 3 x2 = 5
- 2 x1 + x2 = 7
Le vecteur (16/5, 3/5, 0, 0) est solution du système, avec Z= 79/5. Il y a dualité forte donc il s’agit de l’optimal global du programme linéaire.
Exercice 2
Prenons le programme linéaire suivant :
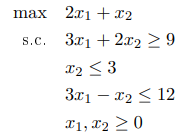
Calculer la solution optimale par résolution graphique. La fonction objectif a pour nouveau coefficient (3, 5), vérifier que la solution trouvée précédemment est toujours optimal à l’aide du dual et des écarts complémentaires.
Le domaine de définition est le suivant :
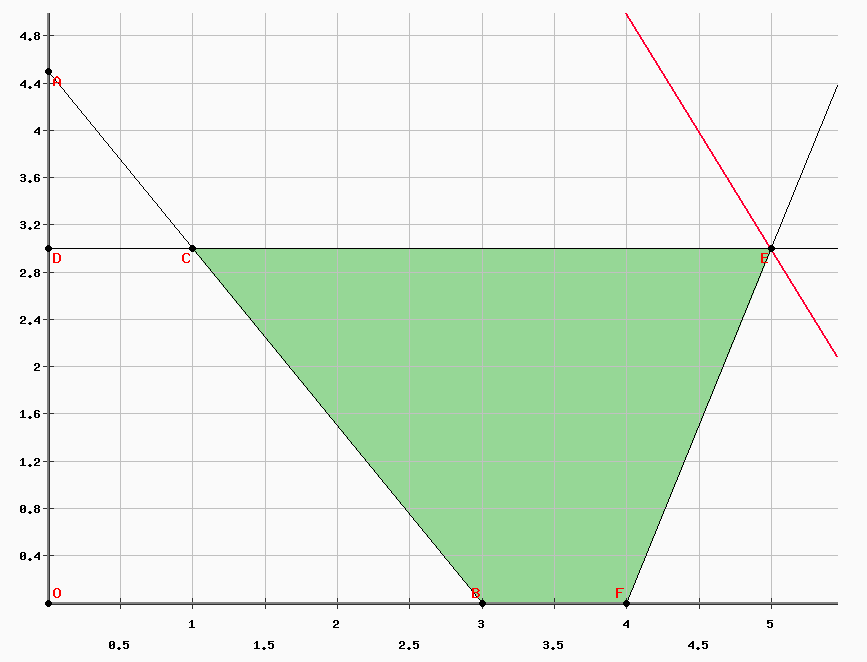
Le solution graphique est le vecteur (5, 3) avec Z=13.
Avec des coefficients de la fonction objectif à (3, 5), nous aurons Z=30. Vérifions avec les écarts complémentaires si nous avons une dualité forte. Le programme dual est le suivant :

Les écarts complémentaires sont les suivants :
- les deux variables de base du primal sont non nulles, donc les deux contraintes du dual sont saturées
- la première contrainte du primal est non saturée, donc la première variable du dual est nulle.
Il faut donc résoudre le système suivant :
- 3 x3 = 3
- x2 – x3 = 5
Le vecteur (0, 6, 1) est solution du système, avec Z= 30. Il y a dualité forte donc (5, 3) est toujours la solution optimale du programme primal.
Exercice 3
Considérons le programme linéaire suivant :
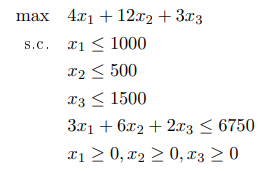
Tester l’optimalité de la solution (250, 500, 1500) à l’aide du dual et des écarts complémentaires.
La modélisation mathématique s’avère fausse, et après vérification le vecteur b des contraintes est (950, 550, 1575, 6900). A l’aide du dual, vérifier si la solution est admissible et s’il s’agit de la solution optimale.
De même avec le vecteur (1000, 500, 1500, 9750).
Le vecteur (250, 500, 1500) est une solution admissible car aucune contrainte n’est violée. La solution optimale a pour valeur Z=11500. Vérifions son optimalité par le dual et les écarts complémentaires. Le dual est le suivant :

Les écarts complémentaires donnent les informations suivantes :
- aucune variable de base du primal n’est nulle, donc les contraintes du dual sont saturées
- la première contrainte du primal n’est pas saturée, donc la première variable du dual est nulle
Cela donne le système suivant :
- 3 X4 = 4
- X2 + 6X4 = 12
- X3 + 2 X4 = 3
Avec pour vecteur solution (0, 4, 1/3, 4/3) avec Z=11500. Il y a dualité forte donc il s’agit bien de la solution optimale.
Testons de nouveau l’optimalité avec un primal avec la colonne b=(950, 550, 1575, 6900), seul la fonction objectif du dual change. La solution est admissible et les écarts complémentaires sont les suivants :
- Les trois variables de base sont non nulles donc les contraintes du dual sont saturées.
- Aucune contrainte n’est saturée, donc les variables de base du dual sont nulles.
Pas besoin de résoudre le dual car les variables de base sont toutes nulles (Z=0), il n’y a pas de solution au dual. Cela signifie que la solution du dual n’est pas sur un extremum du domaine de définition.
De même avec le vecteur b= (1000, 500, 1500, 9750). La solution est admissible et les écarts complémentaires donnent les informations suivantes :
- Les trois variables de base sont non nulles donc les contraintes du dual sont saturées.
- La première et la quatrième contraintes sont non saturées, donc la première et la quatrième variable de base du dual sont nulles.
Le système n’admet pas de solution, donc la solution proposée n’est pas sur un extremum du domaine de définition. Par conséquent il ne peut pas être l’optimum du programme linéaire.
Exercice 4
Lors de l’injection d’une quantité d’électricité dans le réseau, cette énergie se diffuse à travers les lignes offrant le moins de résistance. Il est possible de connaître les lignes qui seront empruntées par ce flux énergétique à l’aide d’un programme linéaire.
Pour cela il faut définir le réseau et le flux énergétique :
- le flux part d’une source unique et se diffuse par le chemin avec le moins de résistance vers le consommateur
- les lignes sont à sens unique, le flux énergétique peut se déplacer que dans le sens du courant transitant déjà sur la ligne
Un réseau est représenté sous la forme d’un graphe comme suivant : les nœuds sont des sous-stations et les arcs représentant les lignes, le nœud 1 est l’origine de la source énergétique, le nœud 7 est la destination du flux énergétique.
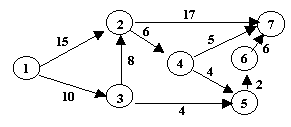
Les variables sont les suivantes :
- pour chaque ligne, une variable comprise entre 0 et 1 donne le pourcentage d’utilisation de la ligne.
La fonction objectif est la suivante :
- on cherche à minimiser le cout total, c’est à dire la somme des pourcentages d’utilisation des lignes multiplié par le cout de la ligne.
Les contraintes sont les suivantes :
- pour le nœud d’origine, la somme des variables des arcs sortants moins la somme des variables des arcs entrants est égale à 1
- pour le nœud d’arrivé, la somme des variables des arcs entrants moins la somme des variables des arcs sortants est égale à 1
- pour les autres nœuds, la somme des variables des arcs sortants moins la somme des variables des arcs entrants est égale à 0.
Représenter le programme linéaire du graphe précédent, calculer le programme dual et le résoudre via Excel. En déduire le résultat du programme Primal, notons qu’un système d’équation peut se résoudre sur Excel par la commande {=PRODUITMAT(INVERSEMAT(Système); Vecteur cible)} où les coefficients sont donnés sous la forme matricielle.
Par exemple :

Le programme linéaire représentant le problème de plus court chemin est le suivant :

Le programme Excel suivant donne les solution du Primal en Vert et les solutions du Dual en Rouge (les contraintes du Primal sont en ligne alors que les contraintes du Dual sont en colonne), noter que les contraintes égalités du Primal font que les variables du dual sont sur l’ensemble des réels :

Les contraintes 4, 5, 7, 8 du dual sont non saturées, donc les variables 4, 5, 7, 8 du primal sont nulles. Il faut donc résoudre le système suivant :

Ce système se résout très simplement sans Excel et à pour réponse le vecteur ( 0, 1, 0, 0, 0, 1, 0, 0, 1, 1) et Z=22. Il y a dualité forte donc c’est une solution optimale. En représentant les arcs utilisés par le flux énergétique en rouge, cela donne le graphe de diffusion suivant :

Exercice 5
Un îlot énergétique (réseau local coupé du réseau global) possède deux sources énergétiques et trois villages consommateurs. La centrale 1 produit 550 MWh et la centrale 2 produit 350 MWh. Le village 1 demande 400 MWh, le village 2 demande 300 MWh et le village 3 demande 200 MWh. Pour chaque MWh transitant sur une ligne du réseau, le coût en euros est suivant le graphe ci-après :

Une solution existe si la quantité disponible est supérieur ou égale à la quantité demandée
- Exprimer le problème de minimisation du coût de transit de l’énergie des producteurs vers le consommateur, expliquer la fonction objectif et les contraintes
- Exprimer le problème de maximisation du profit de transit de l’énergie (point de vue du gestionnaire du réseau).
- Résoudre un des problèmes et trouver une solution de l’autre à l’aide des écarts complémentaires.
Il y a 900 de quantité disponible et autant de demandes, donc il y a une solution possible. Les variables sont les suivantes :
- pour chaque ligne, X représente la quantité transitant par la ligne.
La fonction objectif est la suivante :
- minimiser le cout total des ressources transitant sur toutes les lignes.
Les contraintes sont les suivantes :
- contraintes de stocks (inférieur ou égale)
- contraintes de demandes (supérieur ou égale).
Le programme linéaire est le suivant :
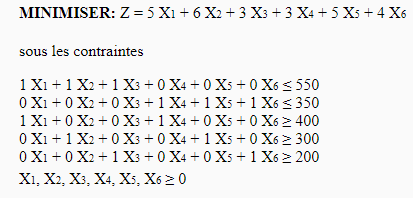
Comme l’exercice précédent, nous allons résoudre le primal et le dual sur la même feuille Excel :
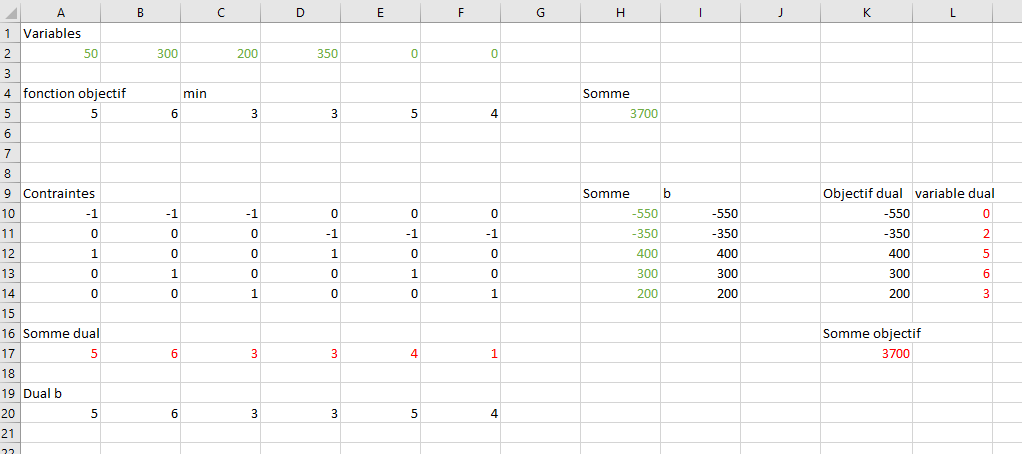
La solution du dual donne pour vecteur solution (0, 2, 5, 6, 3) avec la cinquième et sixième contraintes non saturées. On en déduit que la première contrainte du primal est non saturée (donc avec une variable d’écart non nulle) et que la cinquième et sixième variables de base sont nulles. Il faut donc résoudre le système suivant :
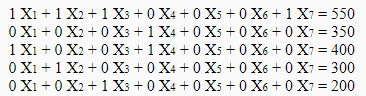
Il est possible de trouver une solution sans Excel, cela donnera le vecteur de base (50, 300, 200, 350, 0, 0) avec Z=3700. Par dualité forte il s’agit d’une solution optimale.
