Contenus
ToggleAnalyse post-optimale de sensibilité
Lorsque la solution de base optimale du problème de PL est analysée pour répondre aux questions relatives aux changements dans sa formulation, l’étude porte le nom d’analyse post-optimale de sensibilité.
On appelle post-optimisation l’ensemble des techniques permettant d’obtenir l’optimum du problème de PL lorsque certaines données ont subi des modifications.
On considère le problème de programmation linéaire général sous sa forme stand art:

Cette étude peut être motivée par plusieurs raisons :
- les données du problème ne sont pas connues avec exactitude, auquel cas il est important de déterminer dans quelle mesure cela affecte la solution proposée;
- on souhaite évaluer les conséquences d’un changement de politique qui modifierait les données du problème.
Coûts marginaux
Si le problème posé consiste à transformer des biens pour vendre une production avec un meilleur profit et l’augmentation maximale de revenu qui résulte de la possibilité de disposer d’une unité supplémentaire de l’un des biens, est la valeur marginale de ce bien. Très souvent, on emploie également dans ce cas le qualificatif coût marginal.
Si une variable d’écart n’est pas nulle, dans la solution optimale, c’est que le bien correspondant est déjà excédentaire. Par conséquent, le fait de disposer d’une unité supplémentaire de ce bien n’aura aucune influence sur le revenu. La variable d’écart a une valeur marginale nulle.
Par contre, si une variable d’écart est nulle dans la solution optimale, c’est que le bien correspondant est totalement utilisé. Par la suite une variation de la disponibilité aura généralement une influence sur le revenu. C’est pourquoi cette variable d’écart nul dans la solution optimale à une valeur marginale non nulle, et cette valeur marginale précise la variation de la fonction économique résultant de l’utilisation d’une unité supplémentaire du bien associé.
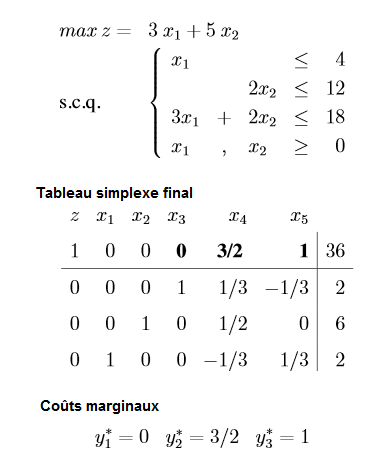
avec comme vecteur solution x* = (2,6). Attention ici la ligne montre la valeur de Z et pas de -Z (d’où les valeurs positives).
On peut mesurer la sensibilité de la solution optimale à un changement d’un terme de droite ou d’un coefficient dans l’objectif.
Étude 1 : variation dans la fonction objectif
La variation d’un coefficient dans la fonction objectif sur un certain intervalle n’entraîne pas de modification de la solution optimale. En dehors de cet intervalle, on a une nouvelle solution qui reste elle-même optimale sur un autre intervalle. On peut ainsi mettre en évidence un nombre fini d’intervalles de variation pour cj, avec sur chacun d’eux une solution invariante.
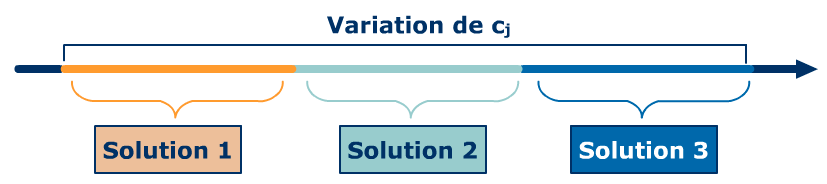
Changeons la fonction objectif par max z’ =4*x1 + 5*x2. La valeur de la fonction objectif évoluera de x*1 = 2, tandis que le vecteur solution ne sera pas modifiée comme le montre la résolution graphique :
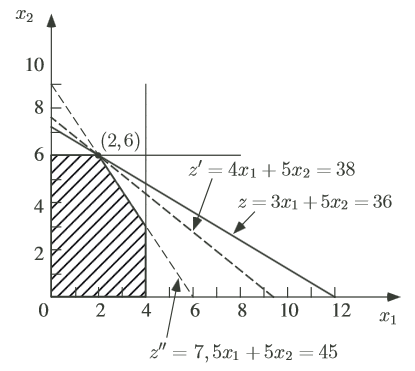
De même si c1 passe de 3 à 2, seule la valeur de la fonction objectif sera modifiée. Pour calculer l’intervalle sur lequel le coefficient x*1 est valide, nous devons faire évoluer la fonction objectif jusqu’à ce qu’elle soit parallèle aux autres contraintes.
C’est-à-dire quand la pente de la fonction objectif est égale à la pente des contraintes saturées pour le vecteur solution s* :
- z = c1*x1 + 5*x2 et 2*x2 = 12 donc -c1/5 = 0, c1 = 0;
- z = c1*x1 + 5*x2 et 3*x1 + 2*x2 = 18 donc -c1/5 = -3/2, c1 =15/2.
Le coefficient x*1 est donc valide pour c1 compris entre 0 et 15/2.
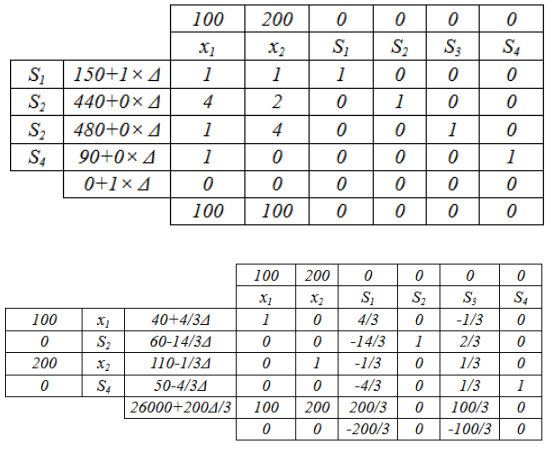
Lorsque le problème est de grande dimension, il est possible de calculer la variation du coût à l’aide du simplexe en ajouter un delta sur le coût à varier comme sur l’exemple suivant :

La solution reste optimal tant que la ligne du -Z a des nombres négatifs donc si :

Étude 2 : variation dans le second membre
Lorsque le second membre d’une contrainte varie (dans un certain intervalle), si cette contrainte n’était pas saturée, alors la solution ne change pas et la valeur optimale de la fonction objectif non plus. Ce résultat est évident puisque la solution optimale ne vérifiant pas avec égalité la contrainte, on peut faire varier (un peu) le second membre sans « toucher » à la solution optimale.
En revanche, si la contrainte était vérifiée avec égalité à l’optimum, on dispose d’un intervalle de variation pour le second membre tel que :
- La solution change mais les variables nulles restent nulles et les variables non nulles restent non nulles : la structure de la solution ne change pas.
- La variation du second membre i entraîne une variation de la valeur optimale de la fonction objectif égale à ui*di, donc proportionnelle à di.
Si on sort de l’intervalle, on a un nouveau coût dual. On peut ainsi mettre en évidence un nombre fini d’intervalles de variation pour le second membre avec, sur chacun d’eux, une valeur pour le coût dual. Sur les différents intervalles, l’analyse de sensibilité ne donne pas la solution optimale puisque les valeurs numériques des variables dépendent de la valeur exacte du second membre.

Considérons dans l’exemple que b1 =4 devient b’1 = 5. Effectuons une résolution graphique du nouveau problème :
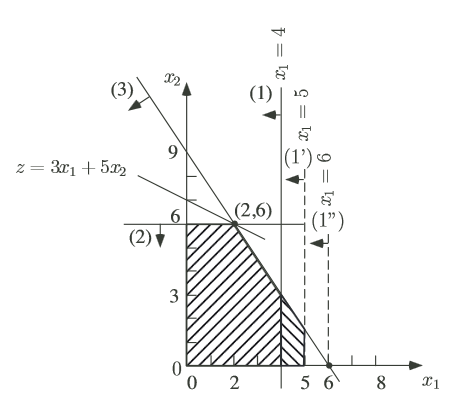
Quand est-il de la diminution de b1 ? Comme l’explication sur les coûts marginaux l’explique, la diminution de 1 du second membre entraîne une diminution de la valeur de la fonction objectif d’un montant égal au coût marginal. Donc la diminution de 1 n’entraînera pas de modification.
Pour connaitre les possibilités d’évolution du stock sans changer la valeur de la solution optimale, il faut rajouter un delta dans le second membre étudié comme le montre l’exemple suivant :
La solution reste optimale tant que le simplexe n’est pas dégénéré, c’est à dire que le second membre est positif :
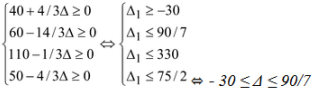
Considérons maintenant une augmentation du troisième second membre à b’3 = 19. Puisque le coût marginal n’est pas nul, la solution optimale sera modifiée comme le montre la résolution graphique.

Étude 3 : variation des variables hors base
Reprenons l’exemple précédent avec une nouvelle contrainte et une nouvelle variable :

Nous avons le coût réduit suivant : d3 = -2. Cela signifie que de construire une unité de x3 diminuerait la valeur de la fonction objectif de 2 (puisqu’elle est hors base x*3 = 0).
Étude 4 : variation de la production
En effet en ajoutant une variable delta dans le coût de la variable en base de la contrainte visé alors il suffit d’injecter le vecteur optimal et résoudre l’équation comme dans l’exemple suivant :

