Contents
ToggleCorrected exercises on relational operators
This page presents use cases for relational operators via corrected exercises.

Course reminder
We want to join two relations R and S (unsorted). R is smaller than S
|R| = Number of pages on disk of R, ||R|| = Number of tuples of R, M = Number of memory pages available (we assume that 3 memory pages are allocated for I/O
Sort-merge join (SMJ) algorithm
Condition on memory | I/O cost |
M > |R|+|S| | Cost = |R|+|S| |
|R|+|S| > M > sqr(|R|+|S|) | Cost = 3|R|+3|S| |
Grace hash join (GHJ) algorithm
Condition on memory | I/O cost |
M > |R| | Cost = |R|+|S| |
M > sqr(|R|) | Cost = 3|R|+3|S| |
Exercise 1
Question 1
Based on the algorithms seen in class, find the cost formulas as well as the limit conditions on the memory (assuming that M does not include 2 or 3 buffers for I/O).
Question 2
Propose an execution strategy for SMJ and GHJ when the memory is smaller than sqr(|R|+|S|) (SMJ) or sqr(|R|) (GHJ)
Question 3
Assuming that to read n consecutive pages from disk takes 10ms + n*0.2ms, compare Block Nested Loop Join (BNLJ), GHJ and SMJ. For the SMJ and the GHJ, we place ourselves in the case where we have a memory smaller than |R|+|S| and that |R| respectively.
Question 4
Based on the Hybrid Hash Join algorithm seen in class, propose an adaptive hashing execution strategy allowing you to take advantage of the maximum available memory but without knowing a priori the size of R (for simplicity, we will assume that M > sqr(|R|) and M<|R|). Evaluate the I/O cost for M = R/2, M = R/3.
Question 1
Based on the algorithms seen in class, find the cost formulas as well as the limit conditions on the memory (assuming that M does not include 2 or 3 buffers for I/O).
SMJ
- M> |R|+|S| : Reading R, sorting R in memory on the join attribute, same for S in memory, merge sorted pages in memory. We therefore have |R|+|S| input output discs to read the 2 relationships. (NB: the writing of the result is never included in the operators' costs).
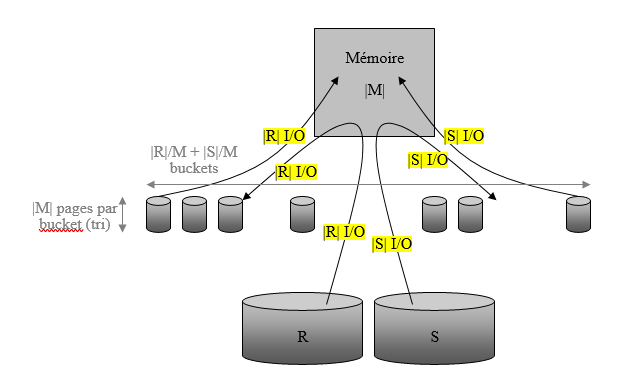
- |R|+|S| > M > sqr(|R|+|S|): The two relations do not hold in memory. The algorithm is then as follows. Read R into memory in packets of M pages and sort the packet in memory on the join attribute. This packet is written on disk (called a bucket in English). The process is repeated |R|/M times until all R has been consumed and sorted.
We obtain |R|/M packets of sorted tuples of R. The number of inputs outputs is therefore here 2|R|, to read R and write the sorted packets of R. The same process is applied to S, corresponding to 2|S| entries exits. We then obtain |R|/M+|S|/M packets of size M. We must then join the tuples. To do this, we carry out the merge phase. We need at least one memory page per packet. The first page of each packet is then recalled in memory. Joining tuples are produced in the result.
When we know that a page of a package contains tuples that can no longer join, we replace it with the next page of the package from which it comes. Thus, each page of each packet is read, generating |R|+|S| entries exits. The number of buckets cannot exceed M if we want to be able to merge. The memory required to perform this processing is at least one page per packet. So it is necessary that M > |R|/M+|S|/M hence the result of the table.
GHJ:
- M> |R|+|S| : Reading R into memory, hashing R, reading and hashing S into memory, joining corresponding hash packets into memory. We therefore have |R|+|S| input outputs.
- M> sqr(|R|): The relation R does not hold in memory. The algorithm is then as follows. Reading R into memory in packets of M and manufacturing N packets of tuples of R hashed on the join attribute (N is the number of hash values produced by the hash function), until having consumed all of R .
The number of buckets of R cannot exceed M to have at least one memory page for each entry in the hash table. The number of inputs and outputs is therefore here 2|R|. The same process is applied to S, generating 2|S| entries exits. To join the tuples, we must read an entire hashed packet of R into memory, and pass the corresponding hashed packet of S page by page. To hold in memory, the hashed packet of R must be less than M. We have at more M packets, and on average |R|/M pages per packet. The memory required to carry out this processing is therefore |R|/M < M hence the result of the table.
Question 2
Propose an execution strategy for SMJ and GHJ when the memory is smaller than sqr(|R|+|S|) (SMJ) or sqr(|R|) (GHJ)
SMJ: we can do several levels of runs. We then increase the size of the packets and reduce their number. This can be done by merging several packets of R (we make larger sorted packets with the tuples of the initial packets) and of S by sorting. We then obtain 3|R|+3|S| I/O (1 run level), 5R|+5|S| (2 levels of runs), 7|R|+7|S| (3 levels of runs).
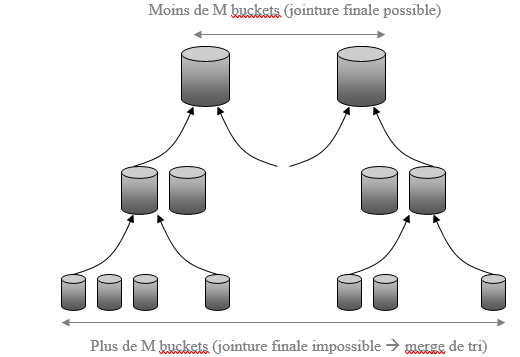
GHJ: We hash more finely (another hashing function) the R packets whose size is greater than that of the memory. (Pb: should we also rehash S?)
Question 3
Assuming that to read n consecutive pages from disk takes 10ms + n*0.2ms, compare Block Nested Loop Join (BNLJ), GHJ and SMJ. For the SMJ and the GHJ, we place ourselves in the case where we have a memory smaller than |R|+|S| and that |R| respectively.
BNLJ: Reads a block of R, then passes all S page by page. Do this R/M times. We therefore obtain: |R|/M (10 + M x 0.2ms) + |R|/M (10ms + |S| x 0.2ms)
SMJ: We obtain 2 x |R|/M (10ms + M x 0.2ms) + 2 x |S|/M (10ms + M x 0.2ms) + (|R|+|S|) (10ms + 0.2ms) = sequential read/write by blocks of R and S + random read of pages of R and S
GHJ: We obtain 2 x (|R|+|S|) (10ms + 0.2ms) + |R|/M (10ms + M x 0.2ms) + |R|/M (10ms + |S| * M / |R| x 0.2ms) = random read/write of pages of R and S + sequential block reading of R and S
Ref: “Seeking the truth about adhoc joins”
Question 4
Based on the Hybrid Hash Join algorithm seen in class, propose an adaptive hashing execution strategy allowing you to take advantage of the maximum available memory but without knowing a priori the size of R (for simplicity, we will assume that M > sqr(|R|) and M<|R|). Evaluate the I/O cost for M = R/2, M = R/3.
We can decide to start hashing R in memory as if everything was going to go well (M > |R|), then as soon as we run out of memory, we put certain hash packets on disk (starting from the end) . These hash values will now be found in the same packet. Then we read S and join with the packets of R found in memory. Tuples of S that join with a packet of R on disk are written to disk as a hash packet. Finally we reread the R and S packets on disk to produce the missing results.
With M=|R|/2, we write half of |R|. At the end, half of the hash packets remain in memory, and on disks the other packets containing half of the tuples of R (|R|/2 inputs outputs). We pass S against the hash table page by page (|S| disk inputs and outputs). We produce the results corresponding to the tuples of S joining with the packets of R in memory and we write the tuples of S to disk (in the form of hash packets). corresponding to R packages on disk.
This generates |S|/2 inputs outputs. Finally, we reread the packets of R and S on disks, which generates |R|/2+|S|/2 inputs and outputs. In total, there are therefore 2 (|R|+|S|) inputs and outputs.
With M=|R|/3, we obtain |R| + 2/3 |R| + |S| + 2/3|S| + 2/3 |R| + 2/3|S| = 7/3 (|R|+|S|) inputs outputs.
Exercise 2
We are now in an extreme case where the available memory is only a few bytes, on the other hand, the data is stored on an electronic memory, the reading cost is therefore similar to reading from memory.
Question 5
Find algorithms and express them with the iterator model formalism to perform the following operations: Selection, projection, join.
Specify the minimum memory required.
Question 6
Can we carry out sorting or aggregate calculations? If yes, how ?
Question 7
You now have a few KB of RAM. How to optimize joins?
Question 8
And sorting or calculating aggregates?
We are now in an extreme case where the available memory is only a few bytes, on the other hand, the data is stored on an electronic memory, the reading cost is therefore similar to reading from memory.
Question 5
Find algorithms and express them with the iterator model formalism to perform the following operations: Selection, projection, join.
Specify the minimum memory required.
The selection and projection operators work tuple by tuple, so they do not consume RAM. The join can be done by nested loop, there is no memory consumption (or 1 pointer per relation).
Question 6
Can we carry out sorting or aggregate calculations? If yes, how ?
We can for example completely scan the operator's input to find the tuple sharing the smallest sort key, then redo a complete scan of the input to deliver all the tuples sharing this key, and so on until having produced all the tuples. We can therefore sort tuples in this way.
To calculate aggregates, we proceed in the same way by calculating the aggregate for the tuples sharing the key.
Question 7
You now have a few KB of RAM. How to optimize joins?
We make a nested loop block…
Question 8
And sorting or calculating aggregates?
We buffer several sorting or aggregate values on each pass on the data. Each pass thus makes it possible to process several sort or aggregate keys.
