Modern datasets are very rich in information with data collected from millions of IoT devices and sensors. This makes for high dimensional data and it's quite common to see datasets with hundreds of features and it's not unusual to see them grow into tens of thousands.
Column/feature selection is a very critical element in a Data Scientist's workflow. When presenting data with very high dimensionality, models usually choke because
- Training time increases exponentially with the number of features.
- Models have an increasing risk of overfitting with an increasing number of features.
- Feature selection methods help solve these problems by reducing the dimensions without much loss of the total information. It also helps to make sense of the features and their importance.

Contents
ToggleSelection of columns
In this page, I discuss the following feature selection techniques and their characteristics.
- Filtering methods
- packing methods and
- Embedded methods.
Filtering methods
The filter methods take into account the relationship between the features and the target variable to calculate the significance of the features.
F Test
F-Test is a statistical test used to compare models and check if the difference is significant between models.
F-Test makes an X and Y hypothesis test model where X is a model created only by a constant and Y is the model created by a constant and a feature.
The least squares errors in the two models are compared and checks whether the difference in errors between models X and Y is significant or introduced by chance.
F-Test is helpful in feature selection as we get to know the importance of each feature in improving the model.
Scikit learn provides top K features using F-Test.
sklearn.feature_selection.f_regressionFor classification type columns:
sklearn.feature_selection.f_classifThere are some downsides to using F-Test to select your features. F-Test only checks and captures linear relationships between features and labels. A highly correlated characteristic receives a higher score and less correlated characteristics receive a lower score.
- The correlation is very misleading because it does not capture strong nonlinear relationships.
- Using crude statistics like correlation can be a bad idea, as Anscombe's quartet illustrates.
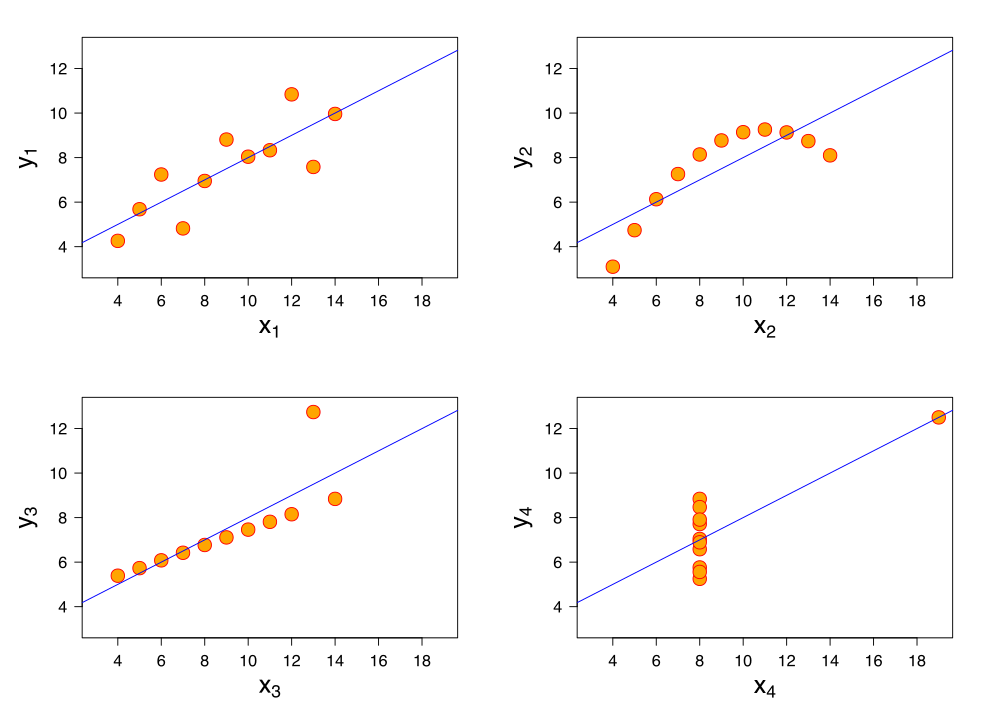
Francis Anscombe illustrates how four separate data sets have the same mean, variance, and correlation to point out that "summary statistics" do not fully describe the data sets and can be quite misleading.
Mutual information
The mutual information between two variables measures the dependence of one variable on another. If X and Y are two variables, and
- If X and Y are independent, no information about Y can be obtained by knowing X or vice versa. Therefore, their mutual information is 0.
- If X is a deterministic function of Y, then we can determine X from Y and Y from X with mutual information 1.
- When we have Y = f(X,Z,M,N), 0 < mutual information < 1
We can select our features from the feature space by classifying their mutual information with the target variable.
The advantage of using mutual information over F-Test is that it works well with the nonlinear relationship between the feature and the target variable.
Sklearn offers a selection of features with mutual information for tasks of regression and classification.
sklearn.feature_selection.mututal_info_regression
sklearn.feature_selection.mututal_info_classif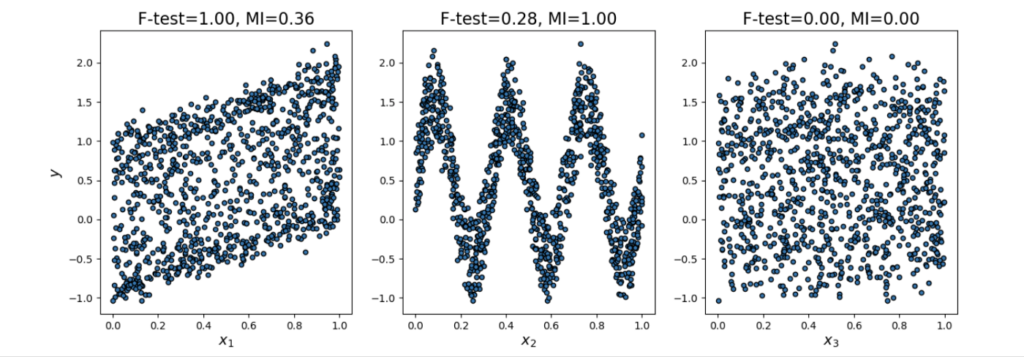
Variance threshold
This method removes features with variation below a certain threshold.
The idea is that when a feature doesn't vary much on its own, it usually has very little predictive power.
sklearn.feature_selection.VarianceThresholdThe variance threshold does not take into account the relationship of the characteristics with the target variable.
Wrapping methods (wrapper)
Wrapper methods generate models with a subset of functionality and measure the performance of their models.
ForwardSearch
This method allows you to find the best feature relative to model performance and add them to your feature subset one at a time.
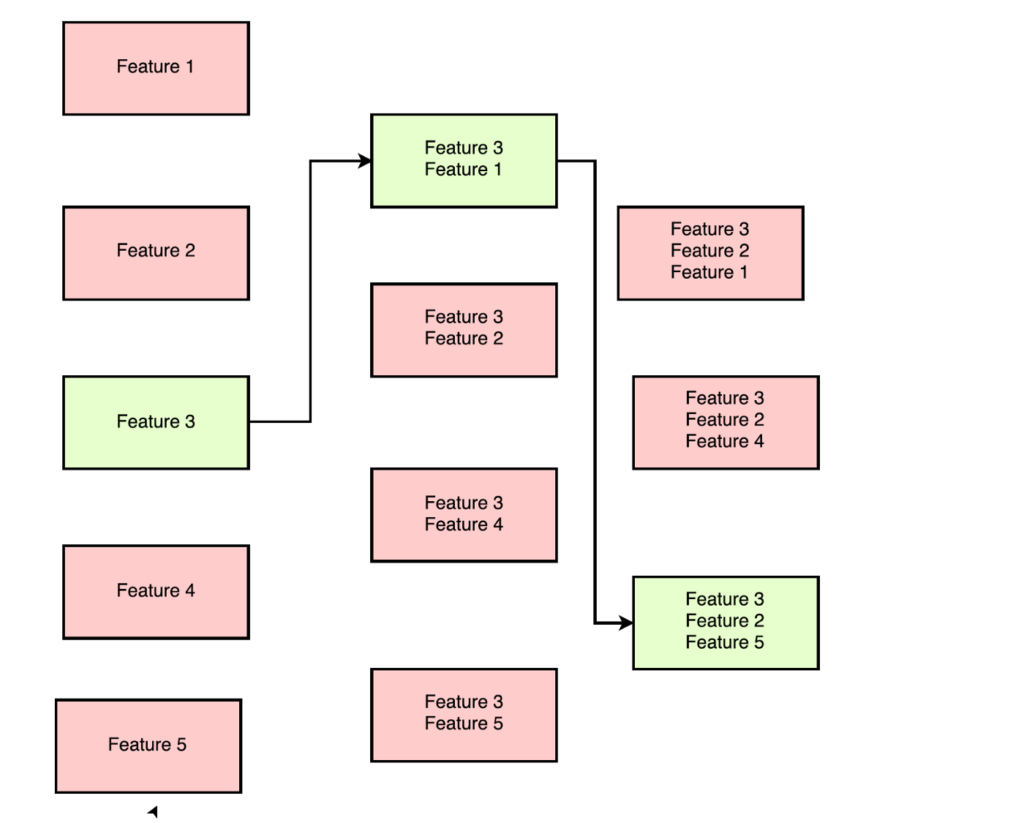
Direct selection method when used to select the best 3 features out of 5 features, features 3, 2 and 5 as the best subset.
For data with n features,
-> In the first round, “n” models are created with individual functionality and the best predictive functionality is selected.
-> In the second round, "n-1" models are created with each feature and the previously selected feature.
->This is repeated until a better feature subset “m” is selected.
Recursive Feature Elimination
As the name suggests, this method eliminates the worst performing features on a particular model one after the other until the best subset of features is known.
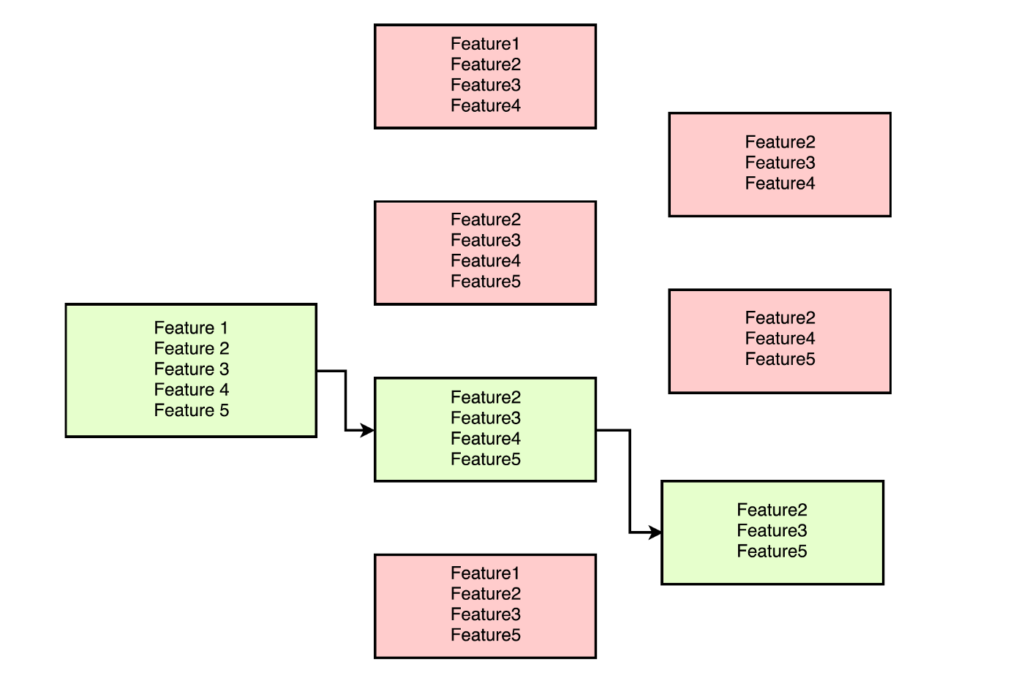
For data with n features,
-> In the first round, “n-1” models are created with a combination of all features except one. Worst performing feature is removed
-> In the second round, the "n-2" models are created by removing another feature.
Wrapper Methods promises you a better feature set with extensive greedy search.
But the main disadvantage of wrapper methods is the amount of models that need to be trained. It is very computationally expensive and impractical with a large number of features.
Embedded methods
Feature selection can also be achieved through information provided by some machine learning models.
LASSO linear regression can be used for feature selections. Lasso regression is performed by adding an extra term to the linear regression cost function. This, in addition to preventing overfitting, also reduces the coefficients of less important characteristics to zero.

Tree-based models calculate feature importance because they need to keep the best-performing features as close to the root of the tree. Build a tree Decision making involves calculating the best predictive characteristic.
Decision trees keep the most important features close to the root. In this decision tree, we find that the number of legs is the most important characteristic, followed by whether it hides under the bed and whether it is delicious, etc.
Feature importance in tree-based models is calculated based on the index of Gini, entropy or chi-square value.
