Red Hopfield

Red Hopfield

En una red de Hopfield, durante el proceso de formación, uno puede pensar que los pesos en la red minimizan una función de energía y se deslizan sobre una superficie de energía. En una red entrenada, cada modelo presentado a la red proporciona un atractor, donde se avanza hacia el punto de atracción mediante la propagación de información por la red.

El objetivo del procesamiento de información del sistema es asociar los componentes de un modelo de entrada con una representación holística del modelo llamado Memoria Direccionable de Contenido (CAM). Esto significa que una vez entrenado, el sistema recordará patrones completos o una versión ruidosa del patrón de entrada.

La red de Hopfield comprende una estructura de datos en grafico con bordes pesados y procedimientos separados para formar y aplicar la estructura. La estructura de la red está completamente conectada (un nodo se conecta a todos los demás nodos excepto a sí mismo) y los bordes (pesos) entre los nodos son bidireccionales.

Los pesos de la red se pueden aprender a través de un método de una sola vez (una iteración en todos los modelos) si se conocen todos los modelos que la red va a memorizar. Alternativamente, los pesos se pueden actualizar de forma incremental usando la regla de Hebb donde los pesos se aumentan o disminuyen según la diferencia entre la salida real y la salida esperada. El cálculo único de los pesos de la red para un solo nodo ocurre de la siguiente manera:

donde w_i, j es el peso entre la neurona i y j, N es el número de modelos de entrada, v es el modelo de entrada y v_ik es el atributo i-ésimo en el modelo de entrada k-ésimo.

La propagación de información a través de la red puede ser asincrónica donde se selecciona un nodo aleatorio en cada iteración, o de forma síncrona, donde la salida se calcula para cada nodo antes de aplicarse a toda la red. La propagación de información continúa hasta que no se realizan más cambios o hasta que se completa un número máximo de iteraciones, después de lo cual se puede leer la plantilla de salida de la red. La activación para un solo nodo se calcula de la siguiente manera:

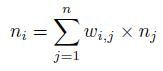
donde n_i es la activación de la i-ésima neurona, w_i, j con el peso entre los nodos i y j, y n_j es la salida de la j-ésima neurona. La activación se transfiere a una salida mediante una función de transferencia, normalmente una función escalonada de la siguiente manera:

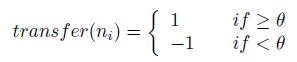
donde el umbral θ generalmente se establece en 0.

La rejilla de Hopfield se puede utilizar para resolver el problema de recordar coincidencias de claves para un patrón de entrada a un patrón asociado previamente aprendido.

La función de transferencia para transformar la activación de una neurona de salida es típicamente una función de paso f (a) en {-1, 1} (preferido), o más tradicionalmente f (a) en {0, 1}. Los vectores de entrada normalmente se normalizan a valores booleanos x en [-1; 1].

La red se puede propagar de forma asíncrona (donde se selecciona un nodo aleatorio y se genera como salida) o de forma síncrona (donde la salida de todos los nodos se calcula antes de aplicarse).

Los pesos se pueden aprender en un método de una sola vez o incremental dependiendo de la cantidad de información conocida sobre los modelos que se van a aprender. Todos los neuronas de la red suelen ser neuronas tanto de entrada como de salida, aunque se han estudiado otras topologías de red (como nombrar neuronas de entrada y salida). Una red de Hopfield tiene límites en los modelos que puede almacenar y recuperar con precisión de la memoria, descritos por N<0.15*n donde N es la cantidad de modelos que se pueden almacenar y recuperar y n es la cantidad de nodos en la red.