Uno de los problemas más comunes que he enfrentado en el limpieza de datos/análisis exploratorio está manejando valores faltantes: cómo tratar con datos faltantes. Primero, comprenda que NO existe una forma correcta de lidiar con los datos faltantes.

Contenido
PalancaCómo lidiar con los datos faltantes: la metodología
Antes de pasar a los métodos de imputación de datos, debemos comprender por qué faltan los datos.
Falta al azar (MAR): Falta al azar significa que la propensión de un punto de datos a perderse no está relacionada con los datos faltantes, sino con algunos de los datos observados.
Missing Completely at Random (MCAR): El hecho de que falte un determinado valor no tiene nada que ver con su valor hipotético y con los valores de otras variables.
Datos no aleatorios faltantes (MNAR): dos posibles razones son que el valor faltante depende del valor hipotético (por ejemplo, las personas con salarios altos generalmente no quieren revelar sus ingresos en las encuestas) o que el valor faltante depende del valor otra variable (por ejemplo, suponga que las mujeres generalmente no quieren revelar su edad! Aquí, el valor que falta en la variable de edad se ve afectado por la variable de sexo).
En los dos primeros casos, es seguro eliminar datos con valores faltantes en función de sus ocurrencias, mientras que en el tercer caso, eliminar observaciones con valores faltantes puede producir un sesgo en el modelo. Por lo tanto, debemos tener mucho cuidado antes de eliminar las observaciones. Tenga en cuenta que la imputación no necesariamente da mejores resultados.
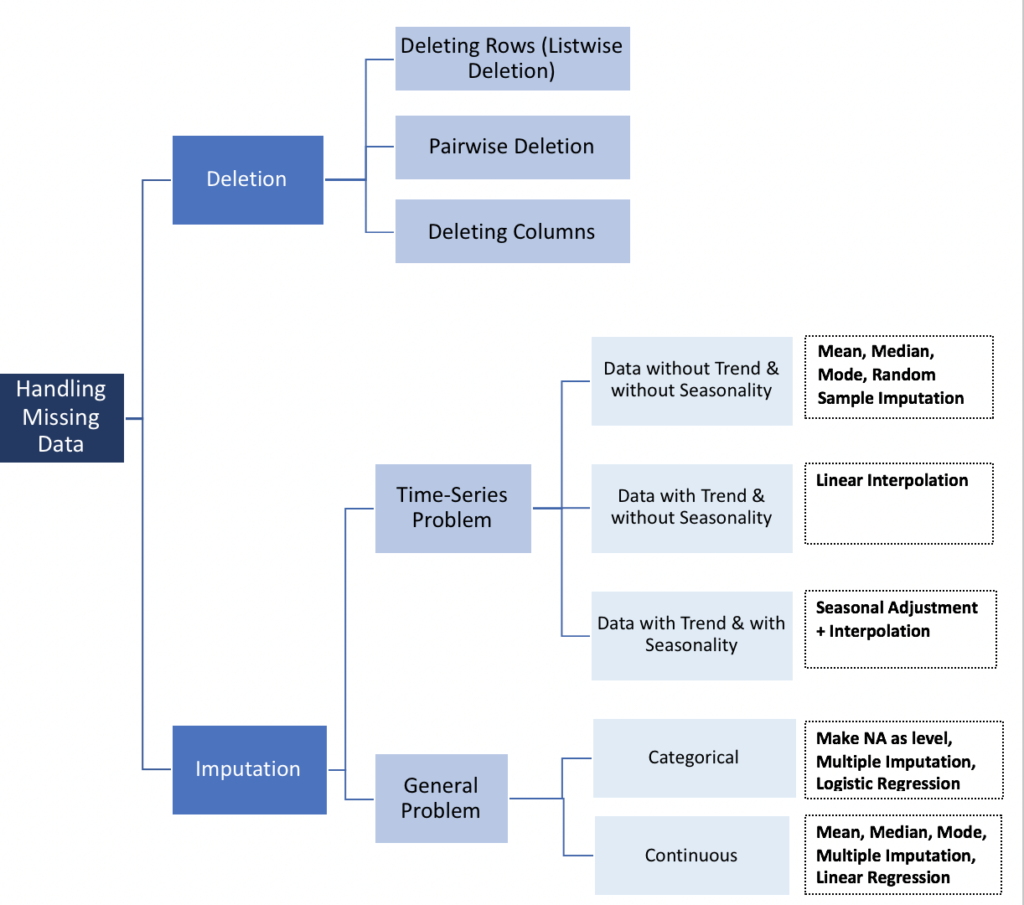
Supresión
- Por lista
Eliminación de lista (análisis de caso completo) elimina todos los datos de una observación que tiene uno o más valores faltantes. En particular, si los datos que faltan se limitan a un pequeño número de observaciones, simplemente puede optar por eliminar estos casos del análisis. Sin embargo, en la mayoría de los casos suele ser una desventaja utilizar la eliminación de listas. De hecho, las suposiciones de MCAR (Missing Completely at Random) son generalmente raras de respaldar. Por lo tanto, los métodos de eliminación de listas producen parámetros y estimaciones sesgados.
nuevosdatos <- na.omit(misdatos)# en pitón
mydata.dropna(inplace=True)
- Por parejas
La eliminación por pares analiza todos los casos en los que están presentes las variables de interés y, por lo tanto, maximiza todos los datos disponibles en una base de análisis. Uno de los puntos fuertes de esta técnica es que aumenta la potencia de su análisis, pero tiene muchos inconvenientes. Se supone que los datos que faltan son MCAR. Si elimina en pares, terminará con un número diferente de observaciones que contribuirán a diferentes partes de su modelo, lo que puede dificultar la interpretación.

#Eliminación por pares
ncovMatrix <- cov(mydata, use="pairwise.complete.obs")#Eliminación por lista
ncovMatrix <- cov(misdatos, use="completo.obs")
- Descartar variables
Siempre es mejor conservar los datos que tirarlos. A veces, puede descartar variables si faltan datos para más de 60 % de casos, pero solo si esa variable es insignificante. Dicho esto, la imputación siempre es una mejor opción que descartar variables.
df <- subconjunto(misdatos, seleccionar = -c(x,z) )
df <- misdatos[ -c(1,3:4) ]en pitón
del mydata.column_name
mydata.drop('column_name', axis=1, inplace=True)
Métodos de series de tiempo
- Última observación realizada hacia adelante (LOCF) y siguiente observación realizada hacia atrás (NOCB)
Este es un enfoque estadístico común para laanálisis de datos medidas longitudinales repetidas donde pueden faltar algunas observaciones de seguimiento. Los datos longitudinales siguen la misma muestra en diferentes puntos en el tiempo. Ambos métodos pueden introducir sesgos en el análisis y dar resultados deficientes cuando los datos muestran una tendencia visible.
- Interpolación linear
Este método funciona bien para una serie temporal con alguna tendencia, pero no es adecuado para datos estacionales.
- Estacionalidad + interpolación
Este método funciona bien para datos con tendencia y estacionalidad.
biblioteca (imputTS)na.random(mydata) # Imputación aleatoria
na.locf(misdatos, opción = "locf") # Última obs. Llevado adelante
na.locf(misdatos, opción = "nocb") # Siguiente obs. llevado al revés
na.interpolation(mydata) # Interpolación lineal
na.seadec(mydata,algorithm="interpolation") # Ajuste estacional luego interpolación lineal
Imputación (métodos convencionales)
Media, mediana y moda
Calcular la media global, la mediana o la moda es un método de imputación muy básico, es la única función probada que no aprovecha las características de la serie temporal ni la relación entre las variables. Es muy rápido, pero tiene inconvenientes obvios. Una desventaja es que la imputación media reduce la varianza en el conjunto de datos.
biblioteca (imputTS)na.mean(misdatos, opción = "media") # Imputación de la media
na.mean(mydata, option = "median") # Imputación de la mediana
na.mean(misdatos, opción = "modo") # Modo de imputaciónen pitón
de sklearn.preprocessing importar imputar
valores = misdatos.valores
imputar = imputar(missing_values='NaN', estrategia='media')
valores_transformados = imputer.fit_transform(valores)La estrategia # se puede cambiar a "mediana" y "más_frecuente"
regresión lineal
Para empezar, se identifican varios predictores de la variable con valores faltantes utilizando una matriz de correlación. Los mejores predictores se seleccionan y utilizan como variables independientes en una ecuación de regresión. La variable con datos faltantes se utiliza como variable dependiente. Los casos con datos completos para las variables predictoras se utilizan para generar la ecuación de regresión; luego, la ecuación se usa para predecir valores faltantes para casos incompletos.
En un proceso iterativo, se insertan los valores de la variable faltante y luego se utilizan todos los casos para predecir la variable dependiente. Estos pasos se repiten hasta que hay poca diferencia entre los valores pronosticados de un paso a otro, es decir convergen.
"Teóricamente" proporciona buenas estimaciones para los valores perdidos. Sin embargo, este modelo tiene varias desventajas que tienden a superar las ventajas. Primero, debido a que los valores sustituidos se predijeron a partir de otras variables, tienden a concordar "demasiado bien" y, por lo tanto, el error estándar se desinfla. También se debe suponer que existe una relación lineal entre las variables utilizadas en la ecuación de regresión cuando puede no haberla.
imputación múltiple
- Imputación: Ingrese m veces las entradas faltantes de los conjuntos de datos incompletos (m = 3 en la figura). Tenga en cuenta que los valores imputados se toman de una distribución. La simulación de dibujo no incluye incertidumbre en los parámetros del modelo. Un mejor enfoque es utilizar la simulación Markov Chain Monte Carlo (MCMC). Este paso da como resultado m conjuntos de datos completos.
- Análisis: Analice cada uno de los m conjuntos de datos completados.
- Agrupación: integre los resultados del análisis m en un resultado final
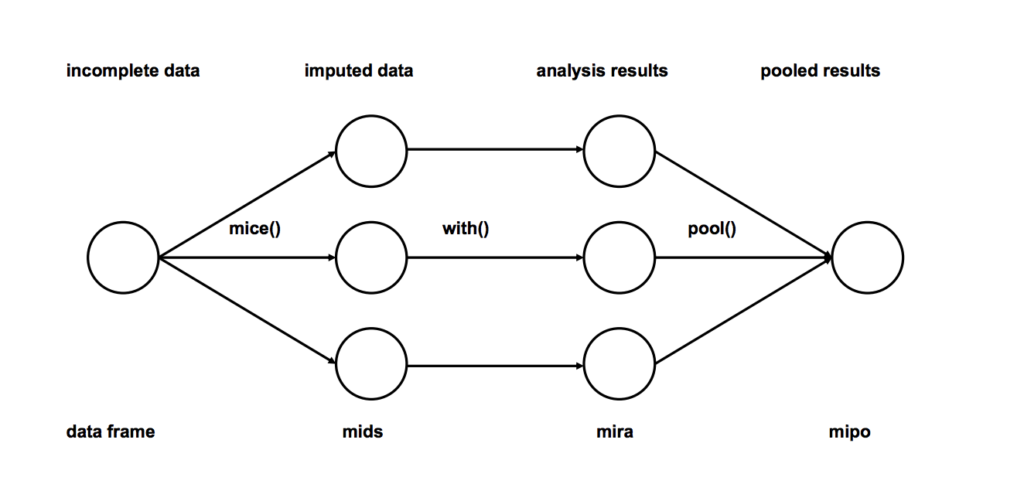
# Usaremos la biblioteca de ratones en r
biblioteca (ratones)
# Regresión determinista imputación a través de ratones
imp <- ratones(misdatos, método = "norma.predecir", m = 1)# Almacenar datos
datos_imp <- completo(imp)
# Imputación múltiple
diablillo <- ratones(misdatos, m=5)Modelo predictivo #build
encajar <- con(datos = imp, lm(y ~ x + z))#combine los resultados de los 5 modelos
combinar <- grupo (encajar)
Este es, con mucho, el método de imputación preferido por las siguientes razones:
- Fácil de usar
- Sin sesgo (si el modelo de imputación es correcto)
Imputación de datos categóricos
- La imputación modal es un método, pero sin duda introducirá un sesgo.
- Los valores faltantes se pueden tratar como una categoría separada en sí misma. Podemos crear otra categoría para valores perdidos y usarlos como un nivel diferente. Este es el método más simple.
- Modelos de predicción: Aquí creamos un modelo predictivo para estimar los valores que reemplazarán los datos faltantes. En este caso, dividimos nuestro conjunto de datos en dos conjuntos: un conjunto sin valores faltantes para la variable (entrenamiento) y otro con valores faltantes (prueba). Podemos usar métodos como la regresión logística y ANOVA para la predicción.
- Imputación múltiple.
Con aprendizaje automático (knn): vea otros cursos para obtener métodos más elaborados
Existen otras técnicas de aprendizaje automático como XGBoost y Random Forest para la imputación de datos, pero hablaremos de KNN ya que se usa ampliamente. En este método, se eligen k vecinos en función de una medida de distancia y su promedio se utiliza como estimación de imputación.
El método requiere la selección del número de vecinos más cercanos y una métrica de distancia. KNN puede predecir atributos discretos (el valor más frecuente entre los k vecinos más cercanos) y atributos continuos (la media entre los k vecinos más cercanos)
La métrica de distancia varía según el tipo de datos:
- Datos continuos: las métricas de distancia comúnmente utilizadas para datos continuos son euclidiana, Manhattan y coseno.
- Datos categóricos: En este caso se suele utilizar la distancia de Hamming. Toma todos los atributos categóricos y para cada uno cuenta uno si el valor no es el mismo entre dos puntos. La distancia de Hamming es entonces igual al número de atributos para los cuales el valor fue diferente.
Una de las características más atractivas del algoritmo KNN es que es simple de entender y fácil de implementar. La naturaleza no paramétrica de KNN le da una ventaja en ciertos contextos donde los datos pueden ser muy "inusuales".
Una de las desventajas obvias del algoritmo KNN es que lleva tiempo analizar grandes conjuntos de datos, ya que busca instancias similares en el conjunto de datos.
Además, la precisión de KNN puede degradarse gravemente con datos de alta dimensión porque hay poca diferencia entre el vecino más cercano y el más lejano.
biblioteca(DMwR)
knnSalida <- knnImputación(mis datos)en pitón
de fancyimpute import KNN
# Use las 5 filas más cercanas que tengan una característica para completar las características faltantes de cada fila
knnSalida = KNN(k=5).complete(misdatos)
De todos los métodos descritos anteriormente, la imputación múltiple y KNN son ampliamente utilizados, y generalmente se prefiere que la imputación múltiple sea más simple.
