Para poder analizar sus datos y realizar cualquier preprocesamiento o reducción, es muy importante normalizar, estandarizar y redimensionar correctamente sus datos. Aquí están los tutoriales.

Contenido
PalancaTutorial sobre cómo normalizar, estandarizar y cambiar el tamaño de sus datos
Antes de sumergirnos en este tema, comencemos con algunas definiciones.
“Redimensionar” un vector significa sumar o restar una constante, luego multiplicar o dividir por una constante, tal como lo haría al cambiar las unidades de medida de datos, por ejemplo, para convertir una temperatura de Celsius a Fahrenheit.
“Normalizar” un vector generalmente significa dividir por una norma del vector. Il fait également souvent référence à la remise à l'échelle par le minimum et la plage du vecteur, pour que tous les éléments se situent entre 0 et 1, amenant ainsi toutes les valeurs des colonnes numériques de l'ensemble de données à une échelle Común.
“Estandarizar” un vector generalmente significa restar una medida de ubicación y dividir por una medida de escala. Por ejemplo, si el vector contiene valores aleatorios con una distribución gaussiana, puede restar la media y dividir por la desviación estándar, obteniendo así una variable aleatoria "normal estándar" con una media de 0 y una desviación estándar de 1.
¿Por que hacerlo?
Estandarización:
Estandarizar características alrededor del centro y 0 con una desviación estándar de 1 es importante cuando se comparan medidas que tienen diferentes unidades. Las variables medidas en diferentes escalas no contribuyen por igual al análisis y pueden terminar creando un sesgo.
Por ejemplo, una variable entre 0 y 1000 tendrá más peso que una variable entre 0 y 1. El uso de estas variables sin estandarización dará como resultado la variable con el peso del rango más amplio de 1000 en el análisis. Transformar los datos a escalas comparables puede evitar este problema. Los procedimientos típicos de normalización de datos igualan el rango y/o la variabilidad de los datos.
Estandarización:
De manera similar, el propósito de la normalización es cambiar los valores de las columnas numéricas del conjunto de datos a una escala común, sin distorsionar las diferencias en los rangos de valores. Para el aprendizaje automático, cada conjunto de datos no requiere normalización. Solo se requiere cuando las características tienen diferentes rangos.
Por ejemplo, considere un conjunto de datos que contiene dos características, edad e ingresos (x2). Donde la edad oscila entre 0 y 100, mientras que los ingresos oscilan entre 0 y 100.000 y más. Los ingresos son unas 1.000 veces superiores a la edad. Así, estas dos características se encuentran en rangos muy diferentes. Cuando hacemos un análisis más profundo, como el regresión multivariado lineal, por ejemplo, el ingreso asignado intrínsecamente influirá más en el resultado debido a su mayor valor. Pero eso no significa necesariamente que sea más importante como predictor. Así que normalizamos los datos para llevar todas las variables al mismo rango.
¿Cuándo hacerlo?
La normalización es una buena técnica para usar cuando no conoce la distribución de sus datos o cuando sabe que la distribución no es gaussiana (una curva de campana). La normalización es útil cuando sus datos tienen escalas variables y el algoritmo que está utilizando no hace suposiciones sobre la distribución de sus datos, como k vecinos más cercanos y redes de neuronas artificial.
La estandarización asume que sus datos tienen una distribución gaussiana (curva de campana). Esto no tiene por qué ser cierto, pero la técnica es más eficiente si su distribución de atributos es gaussiana. La estandarización es útil cuando sus datos tienen escalas variables y el algoritmo que está utilizando hace suposiciones acerca de que sus datos tienen una distribución gaussiana, como regresión lineal, regresión logística y análisis discriminante lineal.
Estandarización
Como vimos anteriormente, la estandarización (o normalización del puntaje Z) significa centrar la variable en cero y estandarizar la varianza en 1. El procedimiento consiste en restar la media de cada observación y luego dividirla por la desviación estándar.
El resultado de la normalización es que las características se escalarán para que tengan las propiedades de una distribución normal estándar con
μ=0 y σ=1
donde μ es la media (media) y σ es la desviación estándar de la media.
StandardScaler de scikit-learn elimina la media y escala los datos por varianza de unidad. Podemos importar el método StandardScaler de sci-kit learn y aplicarlo a nuestro conjunto de datos.
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() data_scaled = scaler.fit_transform(data)
Ahora vamos a comprobar los valores de media y desviación estándar.
print(data_scaled.mean(axis=0)) print(data_scaled.std(axis=0))
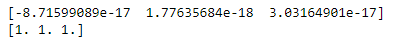
Como era de esperar, la media de cada variable ahora está alrededor de cero y la desviación estándar se establece en 1. Entonces, todos los valores de las variables están en el mismo rango.
print('Valores mínimos (Importe del Préstamo, Tasa Int y Cuota): ', data_scaled.min(axis=0)) print('Valores Máx. (Importe del Préstamo, Tasa Int y Cuota): ', data_scaled.max (eje=0 ))
Sin embargo, los valores mínimo y máximo varían según la dispersión inicial de la variable y están fuertemente influenciados por la presencia de valores atípicos.
Estandarización
En este enfoque, los datos se escalan en un rango fijo, generalmente de 0 a 1.
A diferencia de la normalización, el costo de tener este rango acotado es que terminaremos con desviaciones estándar más pequeñas, lo que puede eliminar el efecto de los valores atípicos. Por lo tanto, MinMax Scalar es sensible a los valores atípicos.
El escalado Min-Max generalmente se realiza a través de la siguiente ecuación:
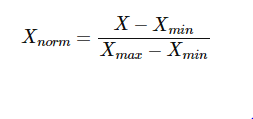
Importemos MinMaxScalar de Scikit-learn y aplíquelo a nuestro conjunto de datos.
from sklearn.preprocessing import MinMaxScaler scaler = MinMaxScaler() data_scaled = scaler.fit_transform(data)
Ahora vamos a comprobar los valores de media y desviación estándar.
print('significa (monto del préstamo, tasa interna y cuota): ', data_scaled.mean(axis=0)) print('std (monto del préstamo, tasa interna y cuota): ', data_scaled.std(axis=0))
Después de MinMaxScaling, las distribuciones no se centran en cero y la desviación estándar no es 1.
print('Min (Importe del Préstamo, Tasa Int y Cuota): ', data_scaled.min(axis=0)) print('Max (Importe del Préstamo, Tasa Int y Cuota): ', data_scaled.max(axis=0))
Pero los valores mínimos y máximos están normalizados entre las variables, a diferencia de lo que sucede con la estandarización.
Escalado robusto
Escalar usando la mediana y los cuantiles consiste en restar la mediana de todas las observaciones y luego dividir por la diferencia intercuartil. Escala características usando estadísticas que son resistentes a los valores atípicos.
La diferencia intercuartil es la diferencia entre el cuantil 75 y el 25:
IQR = cuantil 75 — cuantil 25
La ecuación para calcular los valores escalados:
X_scaled = (X — X.median) / IQR
Primero, importe RobustScalar desde Scikit learn.
from sklearn.preprocessing import RobustScaler scaler = RobustScaler() data_scaled = scaler.fit_transform(data)
Ahora verifique los valores de media y desviación estándar.
print('significa (monto del préstamo, tasa interna y cuota): ', data_scaled.mean(axis=0)) print('std (monto del préstamo, tasa interna y cuota): ', data_scaled.std(axis=0))
Como puede ver, las distribuciones no están centradas en cero y la desviación estándar no es 1.
print('Min (Importe del Préstamo, Tasa Int y Cuota): ', data_scaled.min(axis=0)) print('Max (Importe del Préstamo, Tasa Int y Cuota): ', data_scaled.max(axis=0))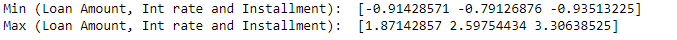
Los valores mínimo y máximo tampoco se establecen en algunos límites superior e inferior como en MinMaxScaler.
