Contenido
PalancaGeneración de columnas
Cuando una programa lineal tiene muchas variables, no es posible resolverlo por un símplex. La generación de columnas permite generar las variables útiles de forma progresiva hasta obtener una solución óptima. El objetivo de este método es resolver un problema reducido con un conjunto limitado de variables.
El problema que consiste en encontrar la mejor variable para agregar en el problema restringido se denomina subproblema asociado al problema maestro (u oráculo). Su objetivo es encontrar la variable (o columna) de mínimo coste reducido (es decir, la más prometedora para mejorar la solución).
El costo reducido de las variables se calcula utilizando las variables duales obtenidas después de resolver el problema restringido. El punto del dual así utilizado en el subproblema se llama punto de separación. A menudo, esta es una solución óptima del problema dual del restringido.
Consideramos el siguiente programa lineal continuo (LP):
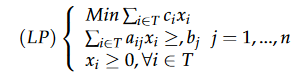
Suponemos que el número de variables en T es demasiado grande para que el problema (LP) se resuelva en un tiempo razonable y que queremos resolverlo generando columnas. Por lo tanto, buscamos resolver el problema restringido asociado con el problema maestro con un conjunto restringido de variables denotadas por Rlos. El problema restringido debe ser factible. Es posible utilizar columnas simples, por ejemplo columnas aleatorias, o incluso las que resultan de una solución factible obtenida de un heurístico.
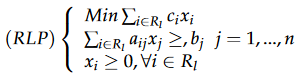
El problema (RLP) ahora es pequeño y será más fácil de resolver con un solucionador. Esta resolución nos proporcionará los valores óptimos de las variables duales vj asociado con restricciones. Estos valores se pasan al subproblema que nos permite obtener la (s) columna (s) para sumar al conjunto Rlos.

El cálculo del coste reducido nos permite saber si una columna disminuyó el valor del objetivo (y por tanto lo mejoró).
Como (LP) es un problema de minimización, el subproblema también busca minimizar este costo reducido. Si el costo mínimo reducido es positivo, entonces no se pueden agregar columnas al problema restringido (RPL) para mejorar el objetivo. La solución óptima del problema restringido es, por tanto, una solución óptima del problema maestro (PL). De lo contrario, agregamos una o más columnas entre las que tienen un costo reducido negativo al actualizar el conjunto Rlos y solucionamos después del nuevo problema restringido (RLP).
