Método PERT: sistemas complejos e inteligencia artificial

Contenido

Método PERT

Como el Gráfico de gantt, el método PERT permite evaluar la duración de la finalización de un proyecto complejo y detectar las partes de este proyecto que no admiten ningún retraso.

La información de la tarea se resume en un programa como el siguiente ejemplo:

Mancha	precedencia	duración
PARA	–	6
B	–	5
VS	PARA	4
D	B	6
mi	VS	5
F	A, D	6
GRAMO	E, F	4

Paso 1: construcción del gráfico a partir de la línea de tiempo

Método PERT - Determinación de niveles de tarea:

Asignaremos el nivel 0 a tareas que no tienen tarea previa.

Asignaremos el nivel 1 a tareas cuyas tareas anteriores están niveladas 0.

De esta forma determinaremos el nivel de cada tarea: tareas de nivel k + 1 Serán las tareas cuyas tareas anteriores sean de nivel inferior con al menos una tarea de nivel k entre ellas.

Construiremos el grafico trazando las tareas en orden ascendente de nivel.

Método PERT: tareas iniciales, finales y convergentes:

Antes de embarcarse en la construcción del gráfico, a menudo será útil detectar las llamadas tareas de inicio, finalización o convergencia.

Las tareas iniciales son tareas sin una tarea previa, comienzan desde arriba 1 del gráfico.

Completar tareas son tareas que no son una tarea previa, llegan al
vértice terminal del gráfico.

Las tareas convergentes son tareas que siempre cumplimos juntos (es decir, nunca una sin la otra) en la columna de tareas anterior; en el gráfico, tendrán el mismo vértice terminal.

método PERT programar niveles de tareas ruta crítica

La cresta entre 2 y 5 se llama tarea ficticia y es siempre de grado cero. Su propósito es modelar el hecho de que la tarea PARA debe completarse para iniciar la tarea F. La cresta entre 1 y 2 significa que la tarea PARA comienza como está 1 y termina como está 2.

Es importante colocar las tareas en orden de ejecución. La tarea F solo se puede colocar después de la tarea PARA y D colocado, y la tarea D solo se puede colocar después de la tarea B. Esto explica la diferencia ficticia entre 2 y 5 (PARA y a distancia 1 entonces que F está en la distancia 3 desde el comienzo).

Paso 2: determina las fechas y los márgenes

Una vez que se ha construido el gráfico, determinaremos las fechas como más temprano y más tarde para el
diferentes vértices y márgenes libres y totales para tareas.

Método PERT - Fechas más tempranas:
Para una cumbre, la fecha más temprana (anotada: t) representa el tiempo mínimo requerido para alcanzar este pico. Se determinará paso a paso, en orden ascendente de vértice, a partir de la entrada del gráfico, gracias al algoritmo de Ford para encontrar el camino más largo.

De este modo :
t₁ = 0 y t_j = Máx (t_I + d_ij ) en todo I anterior j con_ij = tiempo entre pico I y j.
En el ejemplo, t₁ = 0, t₂ = 0 + 6 = 6, t₃ = 0 + 5 = 5, t₄ = 6 + 4 = 10, t₅ = máx. (6 + 0, 5 + 6) = 11, t₆ = máx. (11 + 6, 10 + 5) = 17, t₇ = 17+4 = 21.

La fecha más temprana de la salida del gráfico representa la duración mínima alcanzable para
todo el proyecto (en el ejemplo, t₇= 21, por lo que el proyecto tendrá una duración máxima de 21 días).

Método PERT - Fechas a más tardar:
Para una cumbre, la última fecha (anotada: T) representa concretamente la fecha en la que se debe alcanzar este estado si no queremos aumentar la duración total del proyecto. Se determinará de forma análoga a t, pero en orden descendente de vértice, desde la salida del gráfico hasta la entrada.

De este modo :
T_no = t_no = Duración del proyecto y T_I = Min (T_j - D_ij ) en todos los j que preceden a i.
En el ejemplo, T₇ = 21, T₆ = 21 - 4 = 17, T₅ = 17 - 6 = 11, T₄ = 17 - 5 = 12, T₃ = 11 - 6 = 5, T₂ = mínimo (11-0, 12-4) = 8, T₁ = mínimo (8-6, 5-5) = 0.
Siempre tendremos t₁ = T₁ = 0 y t Menos que o igual a T para cualquier cumbre. Llamamos tt la
margen de flotación superior.

Método PERT - Márgenes de tareas:
El margen libre de una tarea representa el retraso máximo posible de una tarea sin retrasar el inicio de las tareas posteriores, tenga en cuenta ML. El margen total de una tarea representa el retraso máximo posible para la finalización de una tarea sin retrasar todo el proyecto, se notará MONTE : ML_ij = t_j - t_I - D_ij y MT_ij = T_j - t_I - D_ij.

Teniendo en cuenta el modo de cálculo, los márgenes siempre serán positivos o nulos y el margen libre de una tarea siempre será menor o igual a su margen total.

Calificamos de crítica, una tarea cuyo margen total es cero. Una tarea crítica no debe retrasarse si no desea aumentar la duración total del proyecto.

Si aumenta la duración de una tarea no crítica, parte de este aumento será absorbido por el margen de la tarea, solo el excedente afectará la duración del proyecto.

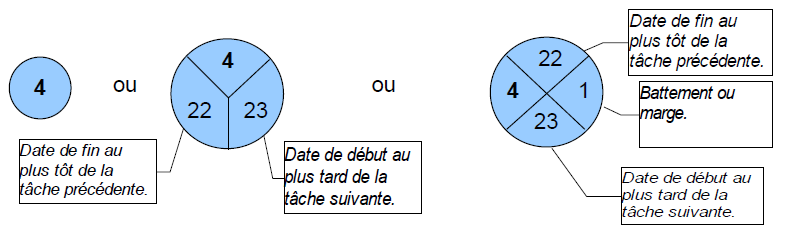
Aparte

Los vértices pueden contener varios datos al mismo tiempo: