Esta página muestra algunos ejercicios corregidos sobre árboles y modelado de teoría de grafos. El objetivo de estos ejercicios es aprender a modelar un problema a través de conceptos básicos y de teoría de grafos.
Modelado con teoría de grafos
Ejercicio 1
Dos jugadores tienen 2 o más lotes de partidos. En cada turno, el siguiente jugador puede eliminar varias coincidencias (según la regla seleccionada). El jugador que elimina el último partido pierde.
Modele este juego con un gráfico en el caso en el que uno tenga dos montones que contengan cada uno tres partidos, y donde un jugador pueda eliminar uno o dos partidos cada uno.
¿Qué movimiento debe jugar el primer jugador para ganar el juego?
Los bordes están orientados de izquierda a derecha. Si estamos en posición o ganamos. Así, la posición comprobará que, sea cual sea la jugada de tu adversario, puedes alcanzar o
Ejercicio 2
El siguiente gráfico muestra los pasillos de un museo. Un guardia colocado en un pasillo puede monitorear dos uniones colocadas en sus extremos. ¿Cuántos guardias se necesitan (y cómo colocarlos) para que se controlen todas las intersecciones?
Si ahora colocamos guardias en las intersecciones, asumiendo que un guardia puede monitorear todos los corredores que conducen a este cruce, ¿cuántos guardias se necesitan?
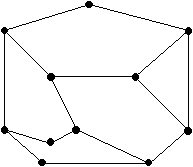
Cada guardia se colocará en un borde y podrá monitorear dos intersecciones (vértices). El gráfico tiene 11 vértices; se necesitarán al menos seis guardias. Por lo tanto, debemos encontrar un conjunto (mínimo) de al menos seis aristas, de manera que cada vértice incida al menos a una de estas aristas. El siguiente gráfico proporciona una solución (bordes más gruesos).
Esta vez, los guardias están en los vértices y vigilan los bordes. Debe haber un conjunto de vértices tal que cada borde incida al menos en uno de estos vértices. El siguiente gráfico proporciona una solución utilizando 6 vértices (vértices blancos).
Ejercicio 4
Skynet es una red con 15 vértices. Puede ir desde cada vértice hasta al menos otros siete vértices por enlace. ¿Podemos ir por enlace desde un vértice X a cada uno de los demás?
Sea A cualquier vértice. X está vinculado a al menos 7 ciudades diferentes. Entonces tenemos una red de 8 vértices conectados por enlaces. En un vértice, también puede conectarse a al menos otros siete vértices; Por tanto, existe una nueva red de 8 vértices. Debe haber un vértice compartido en estas redes, porque de lo contrario la red tendría al menos 16 vértices. X está conectado a A como máximo en dos planos, a través de este vértice común; está conectado con todas las demás ciudades.
Ejercicio 5
Una red está compuesta por siete plantas. Una ciudad está vinculada exactamente a dos plantas. Dos plantas comparten exactamente una ciudad. ¿A cuántas ciudades da servicio la red? Demuestre que una gráfica completa con vértices tiene n (n-1) / 2 enlaces.
Las plantas son los vértices y las ciudades están representadas por un borde que conecta dos vértices. La regla 2 implica que no hay aristas múltiples y que cualquier par de vértices son adyacentes; es decir, que el gráfico esté completo; es k7, es decir, 21 enlaces.
Ejercicio 6
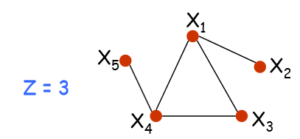
Considerando el siguiente sistema matemático:
Donde es 0 o 1. Determine, con un problema gráfico, una solución que maximice la función objetivo :.
El vértice representa una variable. Dos vértices están conectados si están en la misma desigualdad. El problema es encontrar un conjunto máximo de vértices donde ningún par de vértices tenga un vínculo directo.
Modelado con árbol
Ejercicio 7
Sea un grafo no orientado con vértices. Demuestre que todas las siguientes propiedades son equivalentes:
- es un arbol
- está conectado y si quitamos un borde, ya no está conectado
- está conectado con el borde
- no tiene ciclo hasta que agregamos una ventaja
- no tiene ciclo con borde
- Solo un camino entre cualquier par de vértices
Ejercicio 8
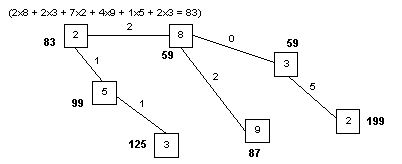
Queremos agregar una batería en una red. El siguiente gráfico muestra el costo de enviar energía entre dos subestaciones de la red y la cantidad de energía enviada por una subestación. Debe colocar la batería en una subestación minimizando el costo total.
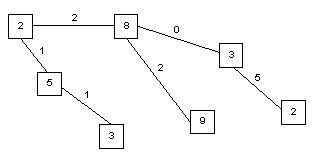
Calcule la suma de todos los costos en cada subestación, es decir, el costo de cada camino entre cualquier subestación a la subestación elegida (borde * vértice).
ES 
FR 
EN