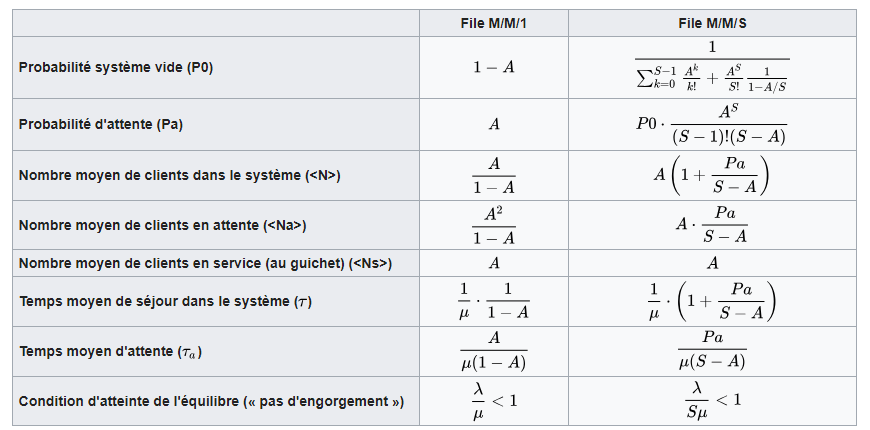
Contenido
PalancaCola M / M / 1
Una cola M / M / 1 sigue una ley exponencial para la llegada y el servicio de los clientes. Una cola M / M / 1 se representa de la siguiente manera:
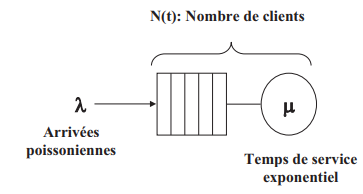
En la mayoría de los casos, el cliente de un servicio está incluido en el número de clientes del cola.
El número de clientes en la cola es modelado por el cadena de markov siguiente tiempo continuo:
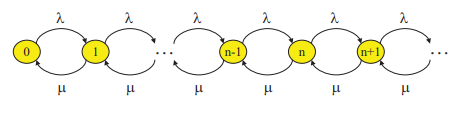
Las probabilidades estacionarias existen porque la cadena es irreducible. Denote por p (n) la probabilidad de que el número de clientes en la cola N (t) = n cuando t tiende a infinito. Las ecuaciones de equilibrio dan el siguiente sistema:
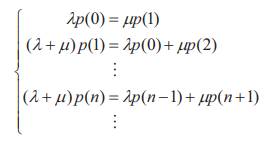
Si establecemos ρ = λ / μ entonces encontramos p (n) = ρnop (0), lo que implica:
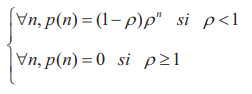
Deducimos que la cola es estable si ρ <1. Es decir, el tiempo medio de procesamiento del cliente es estrictamente menor que el tiempo medio de llegada de un cliente (es decir, el tiempo medio entre la llegada de 2 clientes). La cola es inestable si ρ≥1, en este caso los clientes se acumulan ad infinitum en la cola.
Todos los parámetros de rendimiento se calculan en estado estable si la cola es estable. Si aplicamos la ley de Little y las medidas de rendimiento a las colas M / M / 1 (y más generalmente a las colas M / M / S), con ρ = A: