Aprendizaje de la cuantificación de vectores

Algoritmo de aprendizaje de cuantificación vectorial

El aprendizaje de la cuantización vectorial está vinculado al mapa de autoorganización que, a su vez, está inspirado en las habilidades de autoorganización de neuronas en la corteza visual.

El objetivo del procesamiento de información del algoritmo de aprendizaje de cuantificación de vectores es preparar un conjunto de vectores de libro de códigos (o prototipos) en el dominio de las muestras de datos de entrada observadas y utilizar estos vectores para clasificar ejemplos no tratados. Se prepara un grupo inicialmente aleatorio de vectores que luego se expone a muestras de entrenamiento.

Una estrategia de ganador se lleva todo se utiliza cuando uno o más de los vectores más similares a un patrón de entrada dado se seleccionan y ajustan para estar más cerca del vector de entrada y, en algunos casos, más lejos del ganador para los finalistas. La repetición de este proceso da como resultado la distribución de vectores de libro de códigos en el espacio de entrada que se aproxima a la distribución subyacente de las muestras en el conjunto de datos de prueba.

El algoritmo de aprendizaje de cuantificación vectorial es una técnica de procesamiento de señales en la que las funciones de densidad se aproximan con vectores prototipo para aplicaciones como la compresión. El aprendizaje de la cuantificación de vectores es similar en principio, aunque los vectores prototipo se aprenden mediante un método supervisado en el que el ganador se lo lleva todo.

El siguiente algoritmo proporciona una pseudocódigo preparar libros de códigos vectoriales utilizando el método de aprendizaje de cuantificación vectorial. Los vectores de libro de códigos se inicializan en pequeños valores de coma flotante o se muestrean de un conjunto de datos disponible. La unidad de mejor coincidencia (BMU) es el vector de libros de códigos del grupo que tiene la distancia mínima a un vector de entrada. Se debe definir una medida de distancia entre patrones de entrada. Para vectores de valores reales, esta suele ser la distancia euclidiana:

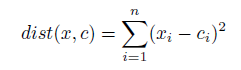
donde n es el número de atributos, x es el vector de entrada y c es un vector de libro de códigos dado.

La cuantificación de los vectores de aprendizaje se diseñó para problemas de clasificación que contienen conjuntos de datos existentes que pueden usarse para supervisar el aprendizaje por parte del sistema. El algoritmo no soporta problemas de regresión. LVQ no es paramétrico, lo que significa que no se basa en suposiciones sobre la estructura de la función a la que se aproxima. Los valores reales en los vectores de entrada deben normalizarse de manera que x esté en [0; 1].

La distancia euclidiana se usa comúnmente para medir la distancia entre vectores de valor real, aunque se pueden usar otras medidas de distancia (como el producto escalar), y es posible que se requieran medidas de distancia específicas de datos para los escalares que no son atributos. Debe haber suficientes iteraciones de entrenamiento para exponer todos los datos de entrenamiento al modelo varias veces. La tasa de aprendizaje suele disminuir linealmente durante el período de aprendizaje a partir de un valor inicial cercano a cero. Cuanto más compleja sea la distribución de clases, se necesitarán más vectores de libro de códigos, algunos problemas pueden requerir miles.

Se sugieren múltiples pasadas del algoritmo de entrenamiento LVQ para un uso más robusto, donde la primera pasada tiene una alta tasa de aprendizaje para preparar vectores de libro de códigos y la segunda pasada tiene una baja tasa de aprendizaje y se ejecuta durante mucho tiempo. iteraciones).