La medida de impureza (Gini) implementa árboles de decisión binarios y las tres medidas de impureza o criterios de división comúnmente utilizados en los árboles de decisión binarios son la impureza de Gini (IG), la entropía (IH) y el error de clasificación (IE).

Contenido
Palancaimpureza de gini
Utilizado por el algoritmo CART (árbol clasificación y regresión) para los árboles de clasificación, la impureza de Gini es una medida de la frecuencia con la que un elemento del conjunto elegido al azar se etiquetaría incorrectamente si se etiquetara al azar en función de la distribución de etiquetas en el subconjunto.
Matemáticamente, podemos escribir la impureza de Gini de la siguiente manera:
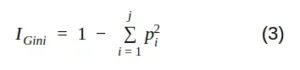
donde j es el número de clases presentes en el nodo y p es la distribución de clases en el nodo.
Simulación sencilla con un conjunto de datos de enfermedades cardíacas que consta de 303 filas y 13 atributos. El objetivo incluye 138 valores 0 y 165 valores 1.
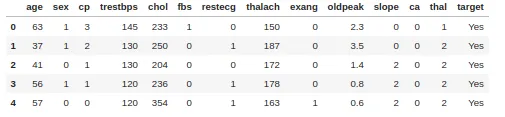
Para crear un árbol de decisión a partir del conjunto de datos y determinar qué separación es mejor, necesitamos una forma de medir y comparar la impureza en cada atributo. El valor de impureza más bajo en la primera iteración será el nodo raíz. podemos escribir la ecuación 3 en la forma:
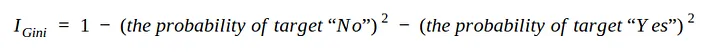
En esta simulación, utilice sólo el sexo, fbs (glucosa en sangre en ayunas), exang (angina inducida por el ejercicio) y atributos objetivo.
Cómo medir la impureza en el atributo Sexo:

- Nudo izquierdo = 0,29
- Nudo derecho = 0,49
Ahora que hemos medido la impureza de ambos nodos de las hojas. Podemos calcular la impureza total con el promedio en peso. El ganglio izquierdo representó 138 pacientes mientras que el derecho representó 165 pacientes.
Impureza total de Gini — Nodo hoja

Procedemos de la misma manera con el resto de atributos:
- I_fbs_izquierda = 0,268; derecha = 0,234; I_fbs = 0,249
- I_exang_left =0,596; derecha = 0,234; I_Exang = 0,399
Fbs (azúcar en sangre en ayunas) tiene la impureza de Gini más baja, así que úselo en el nodo raíz.
Impureza de Gini en datos cuantitativos.
Como el peso que es uno de los atributos para determinar enfermedades cardíacas, por ejemplo tenemos el atributo peso:

Después de ordenar en orden ascendente, haga el promedio par consecutivo y calcule la impureza para cada valor.
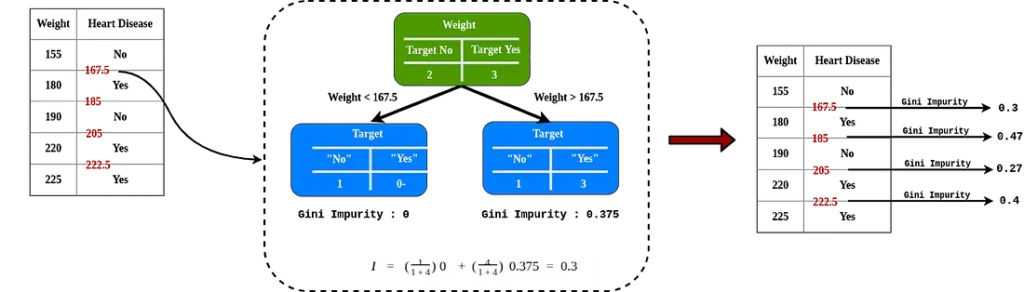
La impureza de Gini más baja es el peso <205, este es el valor umbral y el valor de impureza si se usa cuando lo comparamos con otro atributo.
Por motivos de cálculo, también es posible hacerlo por cuantiles.
Impureza de Gini en datos cualitativos.
Tenemos un atributo de color preferido para determinar el género de una persona:

Para saber qué tan impureza es este atributo, calcule una puntuación de impureza para cada uno (como un valor booleano), así como para cada combinación posible.
entropía
Utilizado por los algoritmos de generación de árboles ID3, C4.5 y C5.0. La ganancia de información se basa en la noción de entropía, la medida de entropía se define como:
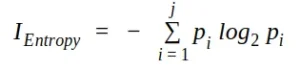
donde j es el número de clases presentes en el nodo y p es la distribución de clases en el nodo.
Dado el mismo caso y conjunto de datos, necesitamos una forma de medir y comparar la entropía en cada atributo. El valor de entropía más alto en la primera iteración será el nodo raíz.
Primero necesitamos calcular la entropía en el atributo Target = 0,994.
Usamos la misma división para el sexo:
- sexo = 0 tiene para la entropía 0,666
- sexo = 1 tiene entropía 0.988
Ahora que hemos medido la entropía de los dos nodos hoja. Tomamos el promedio de los pesos para calcular el valor de entropía total.

Entropía para la columna Fbs = 0,389
Entropía para la columna Exang = 0,224
Fbs (azúcar en sangre en ayunas) tiene la entropía más alta, por lo que lo usaremos en el nodo raíz, exactamente los mismos resultados que obtuvimos con la impureza de Gini.
Error de clasificación/impureza de clasificación errónea
Otra medida de impureza es la impureza por clasificación errónea o error de clasificación errónea. Matemáticamente, podemos escribir la impureza de clasificación errónea de la siguiente manera:
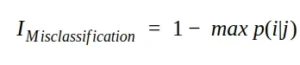
En términos de desempeño cualitativo, este índice no es la mejor opción porque no es particularmente sensible a diferentes distribuciones de probabilidad (que pueden fácilmente llevar la selección hacia la subdivisión usando Gini o entropía).
