Algoritmo estrella: sistemas complejos e inteligencia artificial

Contenido

Algoritmo de estrella

La idea del algoritmo A star o A star o A * es evitar desarrollar caminos considerados demasiado costosos en comparación con los conocidos. Para ello, el algoritmo se referirá a una función para evaluar su costo total. El principio es similar a branch & bound o branch & price.

Función de evaluación

Sea f (n) una función de evaluación para un vértice no, h(n)a heurístico costo estimado para llegar a un estado final, y g(n) el costo real para llegar a la cima no. Entonces f (n) = h (n) + g (n). La función f (n) se puede describir como el costo total estimado para pasar a un estado final a través de no.

La heurística debe ser admisible, es decir, h (n) ≤h '(n) donde h' (n) es el verdadero costo a partir de no hacia un estado final. La heurística nunca sobreestima la distancia real. Y es consistente, es decir, para todo y que desciende de x, h (x) ≤h (y) + costo (xay).

Algoritmo de estrella

Nota s el estado inicial, T el conjunto de estados terminales, k (x, y) el costo de X Para y, F el conjunto de estados desarrollados - cuyos sucesores se han generado (conjunto de cerrados) - y O el conjunto de estados generados pero no desarrollados. El algoritmo de una estrella es el siguiente:

O Siempre que O <> Ø extraiga de O el elemento x tq f (x) es mínimo; Inserte x en F;
    sí x pertenece a T entonces Terminado: Solución encontrada
    De lo contrario
      Por todo y sucesor de x do
        sí y no pertenece a F U O o g (y)> g (x) + k (x, y) entonces g (y) End If
      Fin para
    Terminara si
  Finalizar mientras / CODIGO +

Ejemplo

Para ilustrar el algoritmo de la estrella A, tomaremos el problema de los 8 acertijos como ejemplo. Este problema es una matriz de 3 * 3 que contiene 8 casillas rellenas con los números del 1 al 8 y una casilla vacía. Cada cuadrado puede moverse a un cuadrado adyacente en la matriz, y solo a un cuadrado vacío. En este caso, permitimos el valor de la caja con la caja vacía. El objetivo del 8-puzzle es ordenar las casillas en orden ascendente de izquierda a derecha y de arriba a abajo de la matriz. Concretamente, es una broma.

La heurística utilizada para este ejemplo es la Distancia de Manhattan. Esta distancia es la suma de los movimientos "en línea recta" a realizar para que cada casilla esté en el lugar correcto. En efecto, es una heurística admisible y consistente porque consideramos que todos los movimientos de las cajas son legales. La función g (n) tendrá el valor no, el número de movimientos realizados para llegar a la configuración no.

Tomemos una configuración aleatoria inicial, tenemos para la primera iteración el siguiente árbol:

algoritmo de ruta más corta A algoritmo de estrella A*

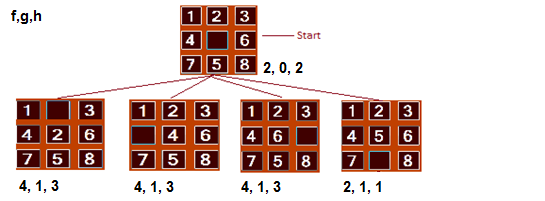
El algoritmo tiene en el conjunto F la raíz y en el conjunto O las 4 configuraciones generadas. La configuración de la derecha tiene la estimación más pequeña del costo total, por lo que se quita de O para ser explorada y finalmente se coloca en F. Obtenemos el siguiente árbol:

Hemos encontrado una solución final tal que su costo es mínimo, el algoritmo de estrella A se detiene.