Contenido
PalancaCriterios de calidad externos
Los índices de calidad externa son índices destinados a medir la similitud entre dos particiones. Sólo tienen en cuenta la distribución de puntos en los diferentes clusters y no permiten medir la calidad de esta distribución.

Lista
- Medición de recuperación de precisión
- Variables indicadoras
- Medida basada en información mutua
- Entropía, pureza y medida V
- Dados Czekanowski
- Folkes-Mallows
- Hubert Γ
- jaccard
- kulczynski
- Mc Nemar
- Fi
- rand
- Rogers-Tanimoto
- Russell Rao
- Sokal-Sneath
Clasificación
Todos los índices propuestos se basan en una matriz de confusión que representa el cómputo de pares de puntos en función de si se consideran pertenecientes o no al mismo cluster según la partición P1 o la partición P2. Por tanto, existen cuatro posibilidades:
• los dos puntos pertenecen al mismo grupo, según P1 y P2
• los dos puntos pertenecen al mismo grupo según P1 pero no según P2
• los dos puntos pertenecen al mismo grupo según P2 pero no según P1
• los dos puntos no pertenecen al mismo grupo, según P1 y P2.
Anotemos yy, yn, ny, nn (y significa sí y n significa no) el número de puntos que pertenecen respectivamente a estas cuatro categorías. Siendo NT el número total de pares de puntos, tenemos:
![]()
Medición de recuperación de precisión y medida F
Si se utiliza la partición P1 como referencia, definimos el coeficiente de precisión como la proporción de puntos precisamente agrupados en P2, es decir que también están agrupados según la partición de referencia P1. Entre los puntos yy + ny agrupados según P2, yy están correctamente agrupados. Entonces tenemos :
![]()
Asimismo, definimos el coeficiente de recuperación como la proporción de puntos agrupados en P1 que también lo están en la partición P2. Se trata de la proporción de puntos que se supone que están agrupados según la partición de referencia P1 y que en realidad están identificados como tales por la partición P2. Entre los puntos yy+yn agrupados en P1, yy también están agrupados en P2. Entonces tenemos :
![]()
En términos de probabilidades condicionales, podemos escribir
![]()
donde los eventos gp1 y gp2 significan que dos puntos se agrupan en P1 y P2 respectivamente.
La medida F es el promedio armónico de los coeficientes de precisión y recuperación:

También existe una versión ponderada de esta medida, llamada medida Fα, definida de la siguiente manera:
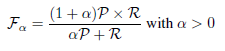
Variables indicadoras
Asociemos a cada partición Pa (a = 1, 2) la variable aleatoria binaria Xa definida sobre el conjunto de índices i y j tal que i < j de la siguiente manera: su valor es 1 si los puntos Mi y Mj están clasificados en la mismo clúster solo en la partición Pa y 0 en caso contrario. La variable Xa funciona como variable indicadora.
Existen NT pares de puntos y sólo nos interesan los índices i y j tales que i < j. Considere la media y la desviación estándar de Xa:
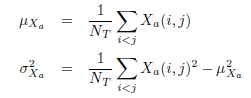
Las siguientes fórmulas relacionan estas variables aleatorias con las variables de conteo coincidentes y discordantes:

De aquí obtenemos:

Medida basada en información mutua
El criterio de información mutua se puede utilizar como una medida externa para la agrupación. La medida para m instancias agrupadas usando C = {C_1,. . . , C_g} y se refiere al atributo objetivo y cuyo dominio es dom (y) = {c_1,. . . , c_k} se define de la siguiente manera:
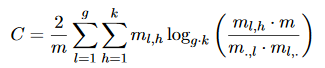
donde m_l, h indica el número de instancias que están en el clúster C_l y también en la clase c_h. m., h indica el número total de instancias en la clase c_h. Asimismo, m_l,. indica el número de instancias del clúster C_l.
MI se combina con entropía en el NMI:

MI se combina con entropía en AMI:
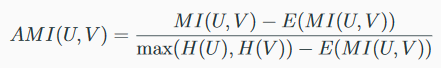
Entropía, pureza y medida V
Dado que el clúster completo (todos los objetos de una misma clase se asignan a un solo clúster) y el clúster homogéneo (cada clúster contiene solo objetos de la misma clase) rara vez se logran, nuestro objetivo es lograr un equilibrio satisfactorio entre estos dos enfoques. Por lo tanto, generalmente aplicamos cinco criterios de agrupación bien conocidos para evaluar el rendimiento de la partición, que son la pureza, la entropía H, la métrica V, el índice RAND y la métrica F. Esta página expone los tres primeros. Los demás están expuestos en otra página.
La medida de entropía se usa para mostrar cómo se dividen los grupos de oraciones dentro de cada grupo, y se conoce como el promedio de los valores ponderados en cada grupo de entropía sobre todos los grupos C = {c_1, …, c_n}:

La pureza de un grupo es la fracción del tamaño del grupo representado por la clase más grande de oraciones asignadas a este grupo, a saber:
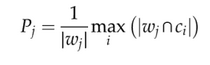
La pureza general es la suma ponderada de las purezas de los grupos individuales dada por:
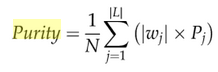
Aunque la pureza y la entropía son útiles para comparar fraccionamiento con el mismo número de grupos, no son confiables al comparar fraccionamiento con diferente número de conglomerados. Esto se debe a que la entropía y la pureza influyen en cómo se dividen los conjuntos de oraciones dentro de cada grupo, y esto conducirá a un caso de homogeneidad. Los puntajes de pureza más altos y los puntajes de entropía más bajos generalmente se obtienen cuando el número total de grupos es demasiado grande, donde este paso conducirá a ser el más bajo en integridad. La siguiente medida considera tanto el enfoque de integridad como el de homogeneidad.
La medida V se conoce como la media armónica de homogeneidad y completitud; es decir, V = homogeneidad * completitud / (homogeneidad + completitud), donde homogeneidad y completitud se definen como homogeneidad = 1-H (C | L) / H (C) y completitud = 1-H (L | C) / H (B) donde:

Dados Czekanowski
El índice de Czekanowski-Dice (también conocido como índice de Ochiai) se define así:
![]()
Este índice es el promedio armónico de los coeficientes de precisión y recuperación, es decir, es idéntico a la medida F:
![]()
Folkes-Mallows
El índice de Folkes-Mallows se define de la siguiente manera:
![]()
Este índice es la media geométrica (raíz cuadrada de la multiplicación) de los coeficientes de precisión y recuperación.
Hubert Γ
El índice de Hubert ˆΓ es el coeficiente de correlación variables indicadoras. Se define de la siguiente manera:
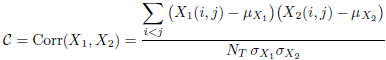
El índice de Hubert ˆΓ aparece como una variante estandarizada (centrada y reducida) del índice de Russell-Rao. Su valor está entre -1 y 1. Podemos escribir el índice ˆΓ de la siguiente manera:
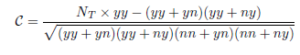
jaccard
El índice Jaccard se define de la siguiente manera:
![]()
kulczynski
El índice de Kulczynski se define de la siguiente manera:
![]()
Este índice es el promedio aritmético de los coeficientes de precisión y recuperación.
Mc Nemar
El índice de McNemar se define de la siguiente manera:
![]()
Bajo la hipótesis nula H0 de que los desajustes entre las particiones P1 y P2 son aleatorios, el índice C sigue aproximadamente una distribución normal. Esta es una adaptación de la prueba no paramétrica de McNemar para comparar frecuencias entre dos muestras pareadas: el estadístico de la prueba de McNemar (llamado distancia χ2) es el cuadrado del índice:
![]()
y sigue, bajo la hipótesis nula de homogeneidad marginal de la tabla de contingencia, una distribución Chi-cuadrado con 1 grado de libertad.
Fi
El índice Phi es una medida clásica de la correlación entre dos variables dicotómicas. Se define de la siguiente manera:
![]()
rand
El índice Rand es un criterio simple que se utiliza para comparar una estructura de agregación inducida (C1) con una estructura de agregación dada (C2). Sea a el número de pares de instancias asignados al mismo grupo en C1 y en el mismo grupo en C2; sea b el número de pares de instancias que están en el mismo grupo C1, pero no en el mismo grupo C2; sea c el número de pares de instancias que están en el mismo grupo C2, pero no en el mismo grupo C1; yd el número de pares de instancias asignados a diferentes clústeres que C1 y C2.
Las cantidades ayd se pueden interpretar como acuerdos y byc como desacuerdos. El índice Rand se define como:
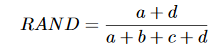
Lo que viene con el sistema de calificación es
(aa+nn)/NT
El índice Rand está entre 0 y 1. Cuando las dos particiones coinciden perfectamente, el índice Rand es 1.
Un problema con el índice Rand es que su valor esperado de dos agrupaciones aleatorias no toma un valor constante (como cero). Hubert y Arabia en 1985 sugieren un índice Rand ajustado que supera este inconveniente.
Rogers-Tanimoto
El índice de Rogers-Tanimoto se define de la siguiente manera:
![]()
Russell Rao
El índice Russell-Rao mide la proporción de coincidencias entre las dos particiones. Se define de la siguiente manera:
![]()
Este índice también se puede escribir:
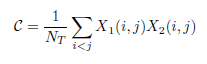
Sokal-Sneath
Hay dos versiones del índice Sokal-Sneath. Se definen respectivamente de la siguiente manera:

