Contenido
PalancaMedidas de distancia para atributos ordinales
Muchos métodos de fraccionamiento use medidas de distancia para determinar la similitud o diferencia entre cualquier par de objetos (como Medidas de distancia para atributos ordinales). Es común denotar la distancia entre dos instancias x_i y x_j como: d(x_i, x_j). Una medida de distancia válida debe ser simétrica y obtiene su valor mínimo (normalmente cero) en el caso de vectores idénticos. La medida de distancia se denomina medida de distancia métrica si también satisface las siguientes propiedades:
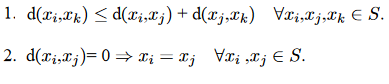
Cuando los atributos son ordinales, la secuencia de valores es importante. En tales casos, los atributos pueden ser tratados como atributos numéricos después de mapear su rango a [0,1]. Este mapeo se puede hacer de la siguiente manera:
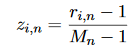
donde z_i, n es el valor normalizado del atributo a_n del objeto i. r_i, n es este valor antes de la normalización y M_n es el límite superior del dominio del atributo a_n (asumiendo que el límite inferior es 1).
