Contenido
PalancaEjercicios corregidos para el problema del camino más corto
Esta página presenta varios ejercicios corregidos sobre el problema de camino más corto. Los ejercicios se enfocan en el camino más corto hacia una fuente y el camino más corto desde múltiples fuentes.

Ejercicio 1
| PARA | B | VS | D | mi | |
| PARA | 1h30 | 2h00 | 2h15 | ||
| B | 1h40 | 3h00 | |||
| VS | 2h20 | 2h55 | |||
| D | 3h20 | 1h05 | |||
| mi | 2h25 | 3h10 | 1h10 |
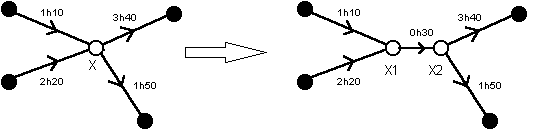
Solo dibuja el grafico, cuyos vértices son las ciudades y los arcos las rutas de la empresa, valorándose en cada arco la longitud del vuelo correspondiente. A algoritmo la ruta más corta resuelve el problema.
Para tener en cuenta la duración de las escalas, son posibles dos métodos: Editar el algoritmo anterior, incluyendo el costo de la escala en los arcos O: se duplica cada vértice; un arco entre ellos es la escala de la ciudad correspondiente.
Ejercicio 2
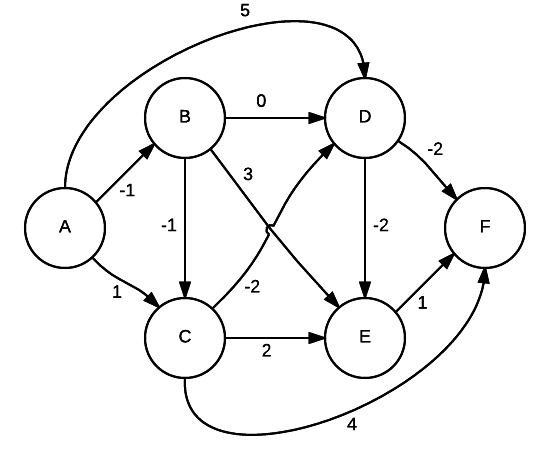
Queremos construir una nueva fábrica en la siguiente red, los nodos son lugares y los enlaces representan los costos para enviar energía de un lugar a otro:

Basado en el algoritmo de Dijkstra, proponga un método para encontrar el mejor lugar para construir la fábrica y luego resuelva el problema con su método. Resolver el problema con el algoritmo de Floyd-Warshall.
Necesitamos calcular Dijkstra para cada nodo (en el nodo de origen). Una vez que se crea el árbol de rutas, agregue el costo de todas las rutas desde cualquier nodo al nodo de origen (agregue la última matriz de rutas más cortas). El mejor lugar es el peso total mínimo de todas las ocurrencias de Dijkstra. Con Floyd-Warshall, la matriz de pseudocierre contiene todos los arreglos, simplemente sume las entradas de cada arreglo y encuentre el mínimo.
Ejercicio 3
Un robot se mueve a través del siguiente entorno. Comienza desde el nodo etiquetado como inicio y debe llegar al nodo etiquetado como final. El entorno es continuo y la escala se proporciona en la figura. Considerando que el robot es un punto, ¿cuál es el camino más corto de principio a fin?
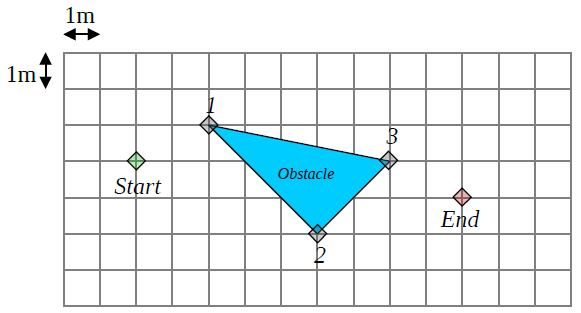
Calcular la distancia euclidiana entre nodos. Dibuje el gráfico y aplique el algoritmo de Dijkstra para encontrar la ruta más corta desde el nodo Estrella hasta el nodo Final. Luego dibuja el camino en la figura.
Camino más corto | Comienzo | 1 | 2 | 3 | Fin |
En eso | 0 | inf | inf | inf | inf |
Comienzo | – | raíz cuadrada 5 | raíz cuadrada 29 | inf | inf |
1 | – | – | raíz cuadrada 29 | sqrt 5+ sqrt 26 | inf |
2 | – | – | – | sqrt 5+ sqrt 26 | raíz cuadrada 29 + raíz cuadrada 17 |
3 | – | – | – | – | raíz cuadrada 29 + raíz cuadrada 17 |
La ruta más corta es Start-2-End.
Ejercicio 4
Considerando la gráfica del ejercicio 1, las aristas se dirigen de izquierda a derecha (o de arriba hacia abajo) y los pesos se reducen en 4. ¿Cómo encontrar un camino mínimo de A a F? Resolver.
Ejercicio 5
(a) Calcule el camino más corto desde s hasta todos los demás vértices utilizando el algoritmo de Dijkstra. Determine el árbol de ruta más corto.
(b) ¿Es único el árbol del camino más corto?
(c) Ahora cambie el peso de la arista (3, 4) a −2. Demuestre que el algoritmo de Dijkstra no funciona en este caso.

(a) La solución viene dada por la siguiente imagen. Los números al lado de los vértices son las distancias al vértice inicial y tachar un número significa que ha habido una actualización. Los números en los cuadrados indican las distancias finales (distancias más cortas).
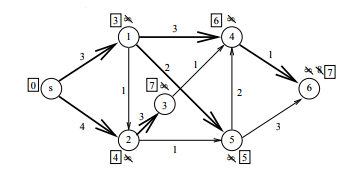
(b) Ninguno árbol el camino más corto es único. Reemplazando la arista (s, 3) por la arista (1, 2) obtenemos otro árbol de caminos más cortos.
(c) El algoritmo de Dijkstra dará la misma solución que en el inciso (a) aunque el camino (s, 1, 2, 3, 4) (dist 5) tiene una distancia más corta que el camino (s, 1, 4) (dist 6). Esto es lo que sucede: después de visitar los vértices s, 1, 2, el algoritmo buscará el camino más corto a un vértice aún no visitado. Este será el vértice 4 con distancia 6. Después de visitar el vértice 4, el algoritmo no se actualizará en el vértice 4 porque ya ha sido visitado y por esta razón no puede encontrar el camino más corto (distancia 5).
Ejercicio 6
Un hombre tiene que llevar un lobo, una cabra y un repollo a través de un río. Tiene un bote para hacerlo, pero es tan pequeño que solo puede llevar una de las tres cosas con él cada vez. ¿Es posible llevar las tres cosas al otro lado del río de forma segura? Tenga en cuenta que el lobo y la cabra o la cabra y el repollo nunca deben estar en el mismo lado del río sin supervisión humana. Al menos el lobo no es vegetariano y no le gusta comer repollo.
Construimos un gráfico para este problema donde cada estado legal está representado por un vértice en el gráfico y encontramos el camino más corto en este gráfico. Sea S = {M,W,G, C} donde M,W,G, C son el hombre, el lobo, la cabra y el repollo.
Un estado para este problema es un par (X, Y) donde {X, Y} es una partición de S. Los elementos de X siempre están en el lado inicial del río y los elementos de Y ya están en el otro lado. Un estado es un estado legal si W,G ∈ X, Y ⇒ M ∈ X, Y y G, C ∈ X, Y ⇒ M ∈ X, Y, no puedes dejar solos el repollo y el lobo o la cabra y el repollo desatendidos .
Construyamos ahora un grafo G = (V, E) que tenga un vértice para cada estado legal de este problema. Tenemos la arista dirigida (v1, v2) ∈ E si podemos pasar del estado v1 = (X1, Y1) al estado v2 = (X2, Y2) en un solo viaje en bote por el río. Todas las aristas tienen un peso ce = 1. Ahora el problema se puede resolver calculando el camino más corto desde el estado (vértice) s = (S, -) hasta el estado (vértice) t = (-, S). Obtenemos 7 como la solución de ruta más corta.
Ejercicio 7
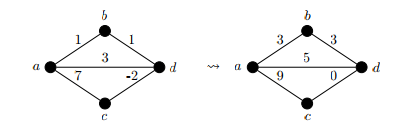
Considere la siguiente modificación del algoritmo de Dijkstra para trabajar con pesos negativos: w(e) = c. Luego, para todas las aristas f en E establecemos w'(f) := w(f) – c. Entonces G'= (V,E,w') no tiene pesos negativos. ¿Esta versión del algoritmo funciona correctamente en este tipo de gráfico? Demuestra tu afirmación.
Ahora afirmamos que el algoritmo no funciona bien en G' porque esta modificación no conserva la propiedad del camino más corto, es decir, (-c) es un número positivo, por lo que suma n veces para obtener un camino n. El siguiente contraejemplo lo demuestra: