Contenido
PalancaAutómata con pilas
Los lenguajes libres de contexto, descritos por gramáticas libres de contexto, son reconocidos (aceptados) por autómatas pushdown. De manera informal, un autómata alimentado por batería es un autómata finito al que se le ha agregado una batería inicialmente vacía de capacidad ilimitada. La ejecución de un autómata pushdown sobre una palabra dada es similar a la de un autómata finito. Sin embargo, en cada paso, el autómata pushdown consulta la parte superior de su pila y eventualmente la reemplaza con una serie de símbolos.
Un autómata a batería es un quintillizo A = (T, P, Q, M, S0) tal que:
- T es el vocabulario terminal,
- P es el vocabulario de la pila (que contiene en particular un símbolo de pila vacío inicial, anotado ⊥),
- Q es un conjunto finito de estados,
- M es un conjunto de transiciones,
- S0 ∈ Q es el estado inicial.
El vocabulario de la pila contiene todos los símbolos que pueden aparecer en la pila y no es necesariamente distinto del vocabulario terminal (podemos tener T ∩ P ≠ ∅).
Una transición de estado a pila es similar a la de una máquina de estado, excepto que además especifica el manejo de la pila. Una transición de M tiene la forma
(estado, symbol_lu, top_stack) → (new_state, action_on_stack) como:
- state y new_state son estados de Q,
- symbol_lu es un símbolo terminal de T, o, lo que significa que el autómata no mira la palabra,
- stack_top es un símbolo de P, o, lo que significa que el autómata no mira en la parte superior de la pila,
- action_on_ stack es:
"Pop el símbolo en la parte superior de la pila", o
"Coloca el símbolo en la parte superior de la pila y luego apila una serie de símbolos" o
"Apila una serie de símbolos", o
"no hacer nada".
El funcionamiento del autómata A = (T, P, Q, M, S0) se define como
siguiente, próximo :
- Una configuración de autómata se caracteriza por un triplete: (S, m, p) con S ∈ Q, m ∈ T∗ y p ∈ P∗ es decir, un estado actual S, una serie m de símbolos terminales (correspondientes al final de la palabra a analizar) y una serie p de símbolos de pila (correspondientes al estado actual de la pila).
La configuración (S0, m0, p0) se puede diferenciar en un paso de la configuración (S, m, p)
(denotado (S, m, p) ⇒ (S0, m0, p0)) si: (S, u, v) → (S0, action_on_pile) es una transición de M, m = u.m0 (la palabra m para analizar comienza con el símbolo u), el símbolo en la parte superior de la pila p es v. p0 es la pila obtenida después de realizar la acción action_on_pile en la pila p.
En otras palabras, el autómata acepta una palabra si hay una serie de transiciones desde el estado inicial y la pila vacía, lo que lleva a la lectura completa de la palabra y nuevamente a la pila vacía. Tenga en cuenta que algunos PLC alimentados por batería pueden aceptar estados finales sin una batería descargada. Además, cualquier autómata que reconoce por estado final tiene un autómata equivalente que reconoce por batería descargada.
Los autómatas alimentados por batería que hemos definido aceptan una palabra cuando hay una rama que conduce a una configuración en la que la pila está vacía y la palabra se lee por completo. Por esta razón, se denominan autómatas apilados que aceptan en una pila vacía. Otra definición de autómatas apilados es la de autómatas apilados que aceptan en el estado final. Tal autómata también especifica un conjunto F ⊆ Q de estados finales. Se acepta una palabra si hay una derivación que conduce a una configuración en la que el estado es final (la pila no necesariamente está vacía).
Hay lenguajes libres de contexto que no son aceptados por ningún autómata push-down determinista. Los lenguajes aceptados por los autómatas deterministas apilados, por lo tanto, forman una subclase de lenguajes libres de contexto: la clase de lenguajes deterministas libres de contexto.
Ejemplo
A continuación se muestra un ejemplo de un autómata apilado no determinista. Deje que el autómata de empuje hacia abajo reconozca el lenguaje de palabras formadas en {a, b} y que contienen el mismo número de a y b: A = (T, P, Q, M, q) tal que: T = {a, b }, P = {a, b}, Q = {q} y la siguiente matriz de transición M
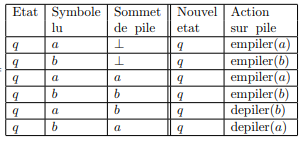
La operación de este autómata sobre la palabra w = aabbabba es:

En cuanto a los autómatas finitos, podemos dar a los autómatas pushdown una representación por grafico. Los arcos tienen la siguiente información:
- símbolo de lectura, símbolo sin apilar; símbolo apilado.
Por ejemplo el arco a, A; ε leerá el símbolo a siempre que pueda colocar un símbolo A en la parte superior de la pila. Tenga en cuenta que ε o λ representan "no hacer nada".
