Retropropagación

Retropropagación

Las redes neuronales feedforward están inspiradas en el procesamiento de información de uno o más células neuronales (llamadas neuronas). Una neurona acepta señales de entrada a través de su axón, que transmite la señal eléctrica al cuerpo celular. Las dendritas transmiten la señal a las sinapsis, que son las conexiones de las dendritas de una célula con los axones de otras células.

En una sinapsis, la actividad eléctrica se convierte en actividad molecular (moléculas de neurotransmisores que cruzan la hendidura sináptica y se unen a los receptores). La unión molecular desarrolla una señal eléctrica que se transmite al axón de las células conectadas. El algoritmo de retropropagación es un régimen de entrenamiento para redes neuronales multicapa con acción directa y no se inspira directamente en los procesos de aprendizaje del sistema biológico.

El objetivo de procesamiento de información de la técnica es modelar una función dada modificando los pesos internos de las señales de entrada para producir una señal de salida esperada. El sistema se entrena mediante un método de aprendizaje supervisado, donde el error entre la salida del sistema y una salida esperada conocida se presenta al sistema y se utiliza para cambiar su estado interno. El estado se mantiene en un conjunto de pesos sobre las señales de entrada.

Los pesos se utilizan para representar una abstracción del mapeo de los vectores de entrada a la señal de salida para los ejemplos a los que se expuso el sistema durante el entrenamiento. Cada capa de la red proporciona una abstracción del procesamiento de información de la capa anterior, lo que permite la combinación de subfunciones y modelado de orden superior.

El algoritmo de retropropagación es un método de aprendizaje de pesos en una red neuronal de retroalimentación multicapa. Como tal, requiere la definición de una estructura de red de una o más capas donde una capa está completamente conectada a la siguiente. Una estructura de red estándar es una capa de entrada, una capa oculta y una capa de salida. El método se refiere principalmente a la adaptación de los pesos al error calculado en presencia de patrones de entrada, y el método se aplica detrás de la capa de salida de la red a la capa de entrada.

El siguiente algoritmo proporciona una pseudocódigo para preparar una red utilizando el método de retropropagación. Se inicializa un peso para cada entrada más un peso adicional para una entrada de polarización constante que casi siempre se establece en 1.0. La activación de una sola neurona en un patrón de entrada dado se calcula de la siguiente manera:

donde n es el número de ponderaciones y entradas, x_ki es el k-ésimo atributo en el i-ésimo patrón de entrada y w_bias es la ponderación de sesgo. Se utiliza una función de transferencia logística (sigmoidea) para calcular la salida de una neurona en [0; 1] y proporciona no linealidades entre las señales de entrada y salida: 1 / (1 + exp (-a)), donde a representa la activación de neuronas.

Las actualizaciones de ponderación utilizan la regla delta, en particular una regla delta modificada en la que el error se propaga hacia atrás a través de la red, comenzando en la capa de salida y ponderado a través de las capas anteriores. A continuación se describe la propagación inversa de errores y actualizaciones de peso para un solo modelo.

Se calcula una señal de error para cada nodo y se envía de vuelta a través de la red. Para los nodos de salida, esta es la suma del error entre las salidas de los nodos y las salidas esperadas:

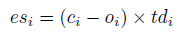
donde es_i es la señal de error para el i-ésimo nodo, c_i es la salida esperada y o_i es la salida real para el i-ésimo nodo. El término td es la derivada de la salida del i-ésimo nodo. Si se utiliza la función de transferencia sigmod, td_i sería o_i * (1-o_i). Para los nodos ocultos, la señal de error es la suma de las señales de error ponderadas de la siguiente capa.

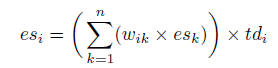
donde es_i es la señal de error para el i-ésimo nodo, w_ik es el peso entre el i-ésimo y el k-ésimo nodos, y es_k es la señal de error para el k-ésimo nodo.

Las derivadas de error para cada peso se calculan combinando la entrada de cada nodo y la señal de error para el nodo.

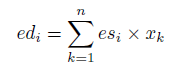
donde ed_i es la derivada de error para el i-ésimo nodo, es_i es la señal de error para el i-ésimo nodo y x_k es la entrada del k-ésimo nodo en la capa anterior. Este proceso incluye el sesgo que tiene un valor constante.

Los pesos se actualizan en una dirección que reduce la derivada de error ed_i (error asignado al peso), medido por un coeficiente de aprendizaje.

donde w_i (t + 1) es el i-ésimo peso actualizado, ed_k es la derivada de error para el k-ésimo nodo y learn_rate es un parámetro de coeficiente de actualización.

El algoritmo de retropropagación se puede usar para entrenar una red multicapa para aproximar funciones no lineales arbitrarias y se puede usar para problemas de regresión o clasificación.

Los valores de entrada y salida deben normalizarse de manera que x esté en [0; 1]. Los pesos iniciales suelen ser pequeños valores aleatorios en [0; 0,5]. Los pesos se pueden actualizar en línea (después de la exposición a cada patrón de entrada) o en lotes (después de que se haya observado un número fijo de patrones). Las actualizaciones por lotes deberían ser más estables que las actualizaciones en línea para algunos problemas complejos.

Una función de transferencia logística (sigmoidea) se usa comúnmente para transferir la activación a un valor de salida binario, aunque se pueden usar otras funciones de transferencia como tangente hiperbólica (tanh), gaussiana y softmax. Se recomienda que exponga el sistema a patrones de entrada en un orden aleatorio diferente en cada iteración.

Por lo general, se utiliza una pequeña cantidad de capas, de 2 a 4, ya que aumentar la cantidad de capas conduce a un aumento en el complejidad del sistema y el tiempo requerido para entrenar las pesas. La tasa de aprendizaje puede variar durante el entrenamiento y es común introducir un término de impulso para limitar la tasa de cambio. Los pesos de una red determinada pueden inicializarse con un método de optimización global antes de refinarse con el algoritmo de retropropagación.

Un nodo de salida es común para problemas de regresión, al igual que un nodo de salida por clase es común para problemas de clasificación.