Contenido
PalancaRegresión y clasificación CART: uso del árbol de decisión
Aquí hay un tutorial para implementar CART. Regresión y Clasificación CART.
Como se ha explicado, los árboles de decisión son el enfoque de aprendizaje supervisado no paramétrico. Además de la clasificación con datos objetivo continuos, también encontramos a menudo casos con datos objetivo discretos llamados regresión. En regresión, la forma más sencilla puede ser utilizar la regresión lineal para resolver este caso. Esta vez la forma de resolver el caso de regresión utilizará una árbol decisión.

CART y mínimos cuadrados para regresión
Para los árboles de regresión, dos medidas de impurezas comunes son:
Mínimos cuadrados. Este método es similar a minimización mínimos cuadrados en un Modelo lineal. Las divisiones se eligen para minimizar la suma residual de cuadrados entre la observación y la media en cada nodo.
Las desviaciones absolutas más pequeñas. Este método minimiza la desviación absoluta promedio de la mediana dentro de un nodo. La ventaja de este método sobre los mínimos cuadrados es que no es tan sensible a los valores atípicos y proporciona un modelo más robusto. La desventaja es la insensibilidad cuando se trata de conjuntos de datos que contienen una gran proporción de ceros.
CART en casos de clasificación utiliza Gini Impurity en el proceso de dividir el conjunto de datos en un árbol de decisión. Por otro lado, CART en casos de regresión utiliza mínimos cuadrados, las divisiones se eligen intuitivamente para minimizar la suma residual de cuadrados entre la observación y la media en cada nodo. Para saber cuál es la “mejor” distribución debemos minimizar el RSS:

Rebanado y optimización
Esta simulación utiliza un conjunto de datos "ficticio" de la siguiente manera

Como se mencionó anteriormente, para conocer la "mejor" distribución, debemos minimizar el RSS. Primero, calculamos RSS dividiéndolo en dos regiones, comenzando con el índice 0
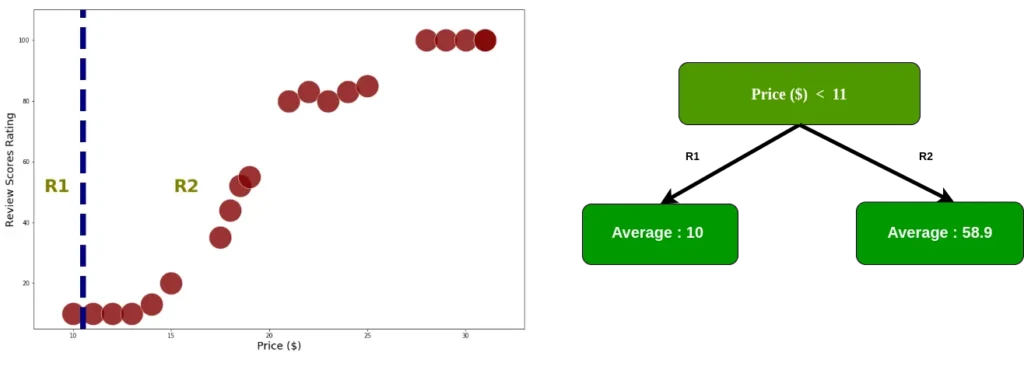
Dado que los datos ya están divididos en dos regiones, agregamos el cuadrado residual para cada dato de índice. Además, calculamos RSS cada nodo usando la ecuación 2.0
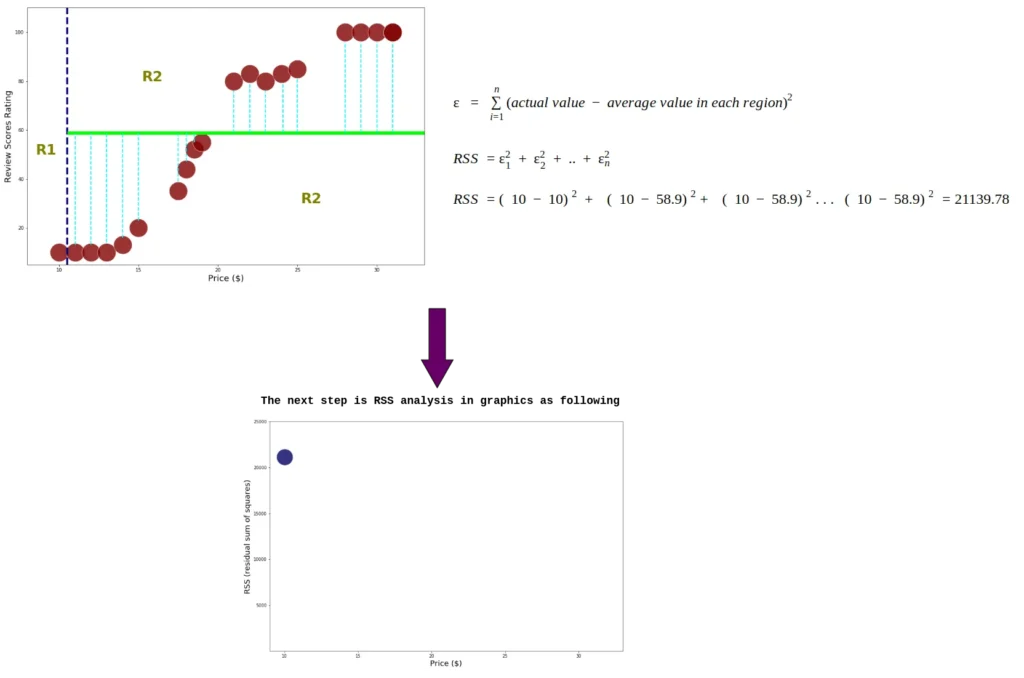
Este proceso continúa hasta que se calcula el RSS en el último índice:

El precio con umbral 19 tiene el RSS más pequeño, en R1 hay 10 datos en precio < 19, por lo que dividiremos los datos en R1. Para evitar el sobreajuste, establecemos los datos mínimos para cada región >= 6. Si la región contiene menos de 6 datos, el proceso de división en esa región se detiene.
Dividir datos con umbral 19

calcular RSS en R1, el proceso en esta sección es el mismo que el proceso anterior, realizado solo para R1. Es posible hacer tantas ramas como desees, ¡ten cuidado de mantener una masa constante de puntos!

Lo que da el siguiente árbol de regresión después de 2 ramas:

Con múltiples columnas
Simplemente calcule el RSS para cada predicador y haga raíz/ramificación del que tenga el RSS más pequeño (¡tenga cuidado de usar preprocesamiento y una métrica adecuada en caso de datos desequilibrados!)
CARRITO para clasificación
Para la clasificación utilizamos elimpureza por Gini. Como ejemplo, tomamos un conjunto de datos sobre enfermedades cardíacas con 303 filas y 13 atributos. El objetivo incluye 138 valores 0 y 165 valores 1.
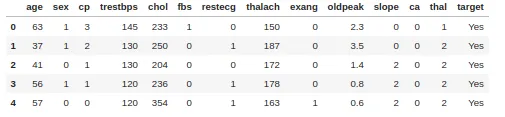
Calculemos la impureza de Gini para la columna Sexo.


Para Fbs tenemos 0.360. Para moneda extranjera 0,381. Fbs tiene la impureza Gini más pequeña, por lo que esta será nuestra raíz.
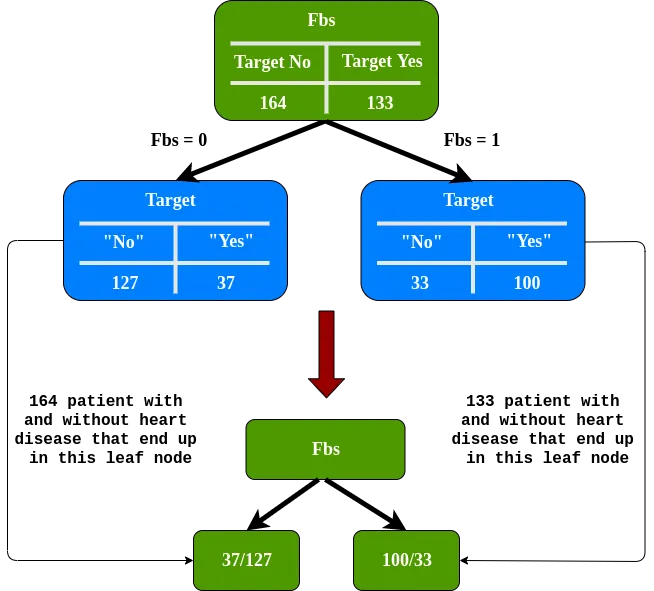
Necesitamos determinar hasta qué punto Sex y Exang separan a estos pacientes en el nodo izquierdo de Fbs.
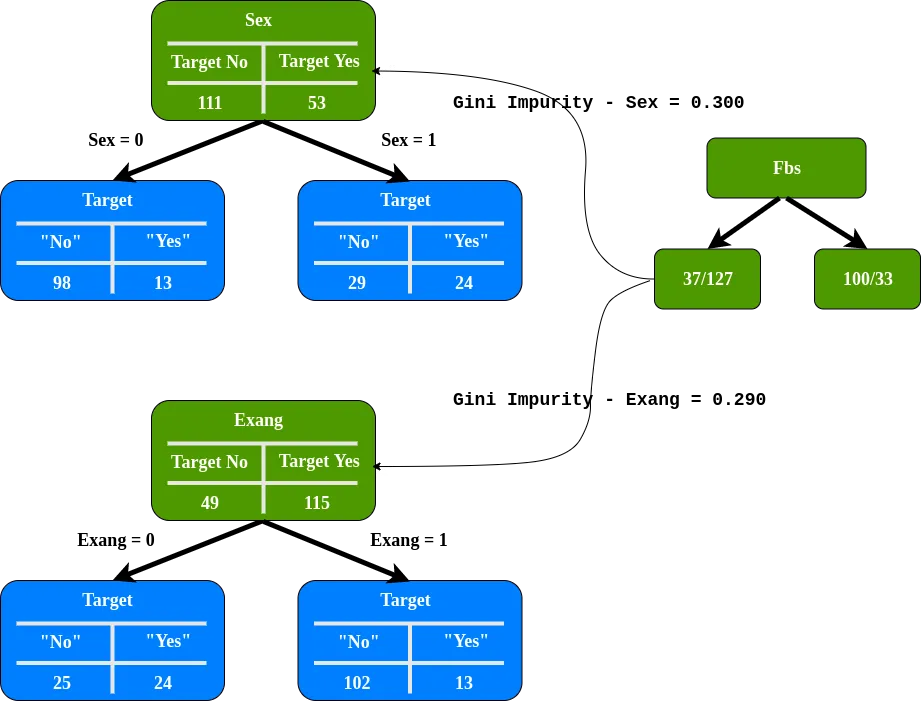
Exang (angina inducida por el ejercicio) tiene la impureza de Gini más baja, la usaremos en este nodo para separar a los pacientes.
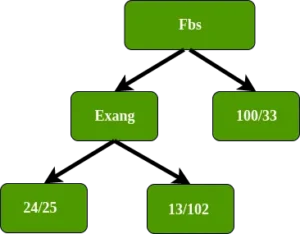
En el nodo izquierdo de Exang, ¿qué distancia separa esto a estos 49 pacientes (24 con enfermedad cardíaca y 25 sin enfermedad cardíaca? Como solo queda el atributo de sexo, colocamos el atributo de sexo en el nodo izquierdo de Exang Exang.
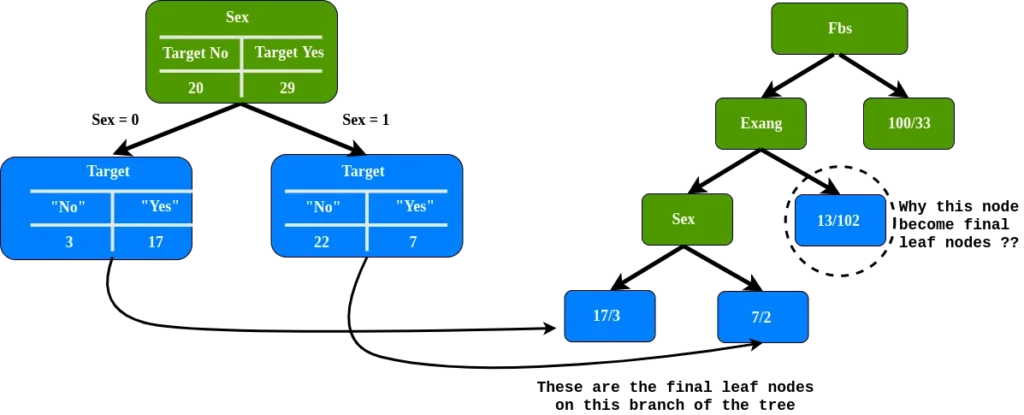
Como podemos ver, tenemos nodos de hoja finales en esta rama, pero ¿por qué está encerrado en un círculo el nodo de hoja, incluido el nodo final?
Nota: el nódulo de la hoja circulado, 89%, no tiene enfermedad cardíaca
¿Estas nuevas sábanas separan a los pacientes mejor que antes?
Para responder a estas preguntas, necesitamos comparar la impureza de Gini usando el atributo de sexo y la impureza de Gini antes de usar el atributo de sexo para separar a los pacientes.

La impureza de Gini antes de usar el género para separar a los pacientes es la más baja, por lo que no separamos este nodo usando el género. El último nodo de hoja en esta rama del árbol. Hacemos lo mismo para la rama derecha de la raíz, lo que da el siguiente árbol de decisión:
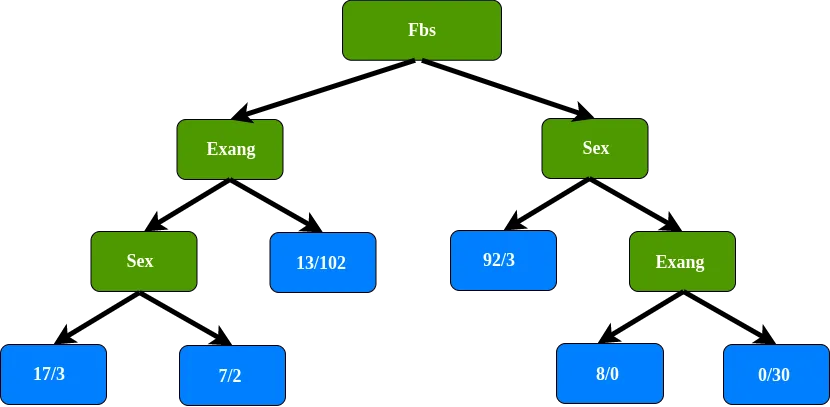
Resumen de clasificación
Punto principal durante el proceso de división del conjunto de datos
1. calcular todos los puntajes de impureza de Gini
Segundo, compare la puntuación de impureza de Gini, después de n antes de usar un nuevo atributo para separar los datos. Si el nodo en sí tiene la puntuación más baja, no tiene sentido separar los datos
3. Si la separación de datos produce una mejora, elija la separación con la puntuación de impureza más baja.
