Esta página presenta un ejercicio corregido detallado del problema de programación lineal resuelto por el algoritmo de rama y atado.

Contenido
PalancaEjercicio corregido paso a paso de bifurcar y acotar
El dueño de un taller de maquinaria planea expandirse comprando nuevas máquinas, prensas y tornos. El propietario estimó que cada prensa comprada aumentará las ganancias en 100 $ por día y cada giro aumentará las ganancias en 150 $ por día. La cantidad de máquinas que el propietario puede comprar está limitada por el costo de las máquinas y el espacio disponible en el taller. Los precios de compra de la máquina y los requisitos de espacio son los siguientes.

El propietario tiene un presupuesto de 40.000 $ para la compra de maquinaria y 200 pies cuadrados de superficie disponible. El propietario quiere saber cuántas máquinas de cada tipo comprar para maximizar el aumento diario de las ganancias. Resuelve este problema.
Solución
El primer paso es modelar el problema, este es un problema lineal como un número entero (por lo que el símplex no puede aplicar).
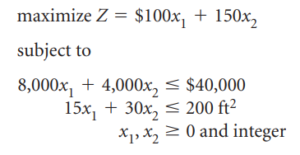
Siendo x_1 el número de pulsaciones y x_2 el número de vueltas.
Comenzamos el método de bifurcación y acotación resolviendo primero el problema como un modelo de programación lineal regular sin restricciones sobre los números enteros (es decir, las restricciones sobre los números enteros se relajan o se relajan). El modelo de programación lineal para el problema y la solución relajada óptima es

La solución óptima relajada es x_1=2.22 y x_2=5.56 con Z=1055.56.
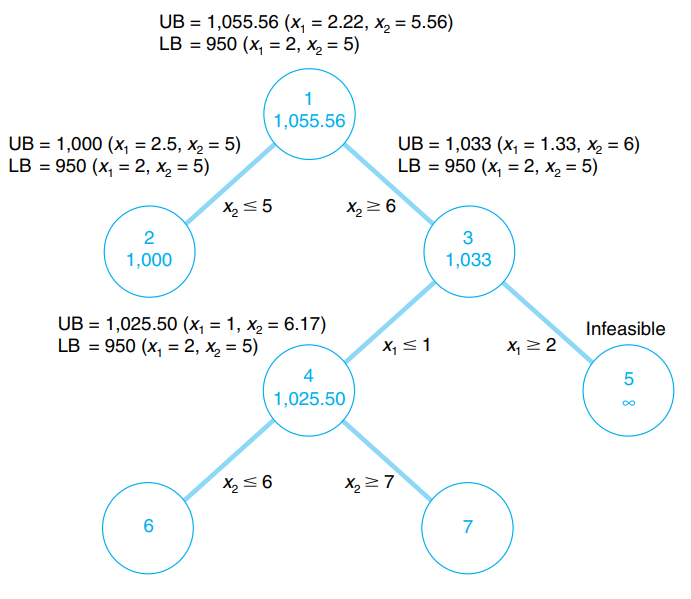
El método de bifurcación y vinculación utiliza un diagrama que consiste en nodos y bifurcaciones como marco para el proceso de solución. El primer nodo en el diagrama de rama y vínculo, que se muestra en la Figura C-1, contiene la solución de programación lineal relajada que se mostró anteriormente y la solución redondeada.
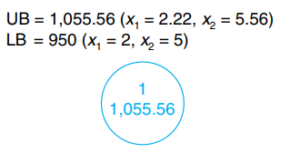
Denotamos límite superior el resultado de la solución óptima relajada y límite inferior el resultado de la solución óptima como un número entero (redondeado hacia abajo).
Primera conexión
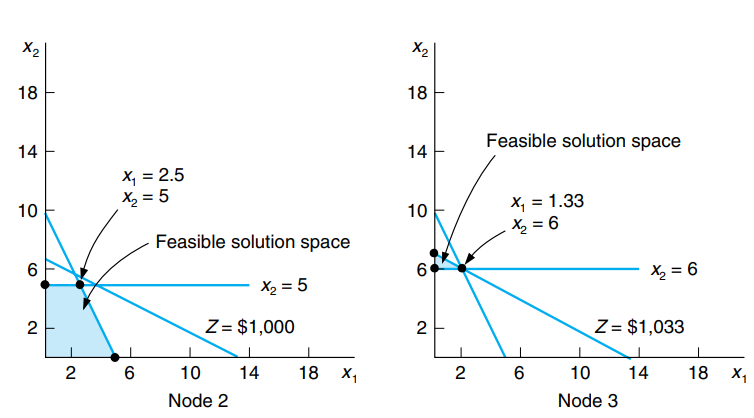
Cree dos restricciones (o subconjuntos) para eliminar la parte fraccionaria del valor de la solución y ver cuál está más lejos del valor entero redondeado (es decir, qué variable tiene la parte fraccionaria más grande en valor absoluto). La parte 0,56 de 5,56 es la parte fraccionaria más grande; por lo tanto, x_2 será la variable a la que vamos a "conectar".
Es decir, crearemos dos programas lineales alternativos teniendo en cuenta respectivamente que x_2 debe ser menor o igual a 5 por un lado; y x_2 debe ser mayor o igual a 6 por otro lado.
Entonces tenemos la siguiente conexión:

Resolvamos el problema de la izquierda:
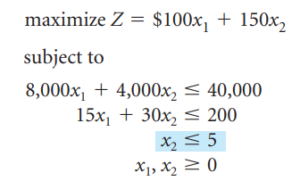
Esto da la solución x_1=2.5, x_2=5 y Z=1000.
Resolvamos el sistema de la derecha:
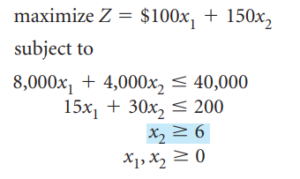
Este sistema tiene por solución x_1=1.33 y x_2=6, Z=1033.33
Desde un punto de vista práctico, cortamos el campo de definición con la restricción x_2=6 y se han resuelto a ambos lados de la restricción que libera el sistema lineal.
Actualicemos nuestro grafico con los nuevos UB y LB de cada sistema obtenidos.
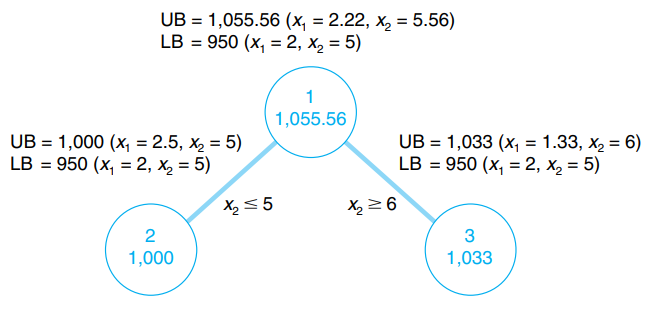
Dado que aún no tenemos una solución entera óptima y factible, debemos continuar ramificando (es decir, dividiendo) el modelo, ya sea desde el nodo 2 o desde el nodo 3. Una mirada a la Figura revela que si ramificamos desde el nodo 2, el el valor máximo que posiblemente se puede alcanzar es 1000 $ (el límite superior).
Sin embargo, si comenzamos desde el nodo 3, es posible un valor máximo más alto de 1033 $. Por lo tanto, nos bifurcaremos desde el nodo 3. En general, siempre bifurquemos desde el nodo con el límite superior máximo.
Segunda conexión
Ahora los pasos de bifurcación seguidos previamente en el nodo 1 se repiten en el nodo 3. Primero, se selecciona la variable que tiene el valor con la parte fraccionaria más grande. Como x_2 tiene un valor entero, x_1, con una parte fraccionaria de 0.33, es la única variable que podemos seleccionar. Por tanto, se desarrollan dos nuevas restricciones a partir de x_1.

Tomando el nodo 4, tenemos el siguiente programa lineal:

La solución al problema es x_1=1 y x_2=6.17 con Z=1025.
El segundo problema es:
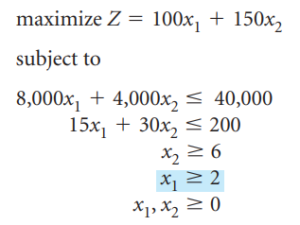
Este problema no admite solución (se viola la primera restricción). Entonces tenemos el siguiente gráfico solución:
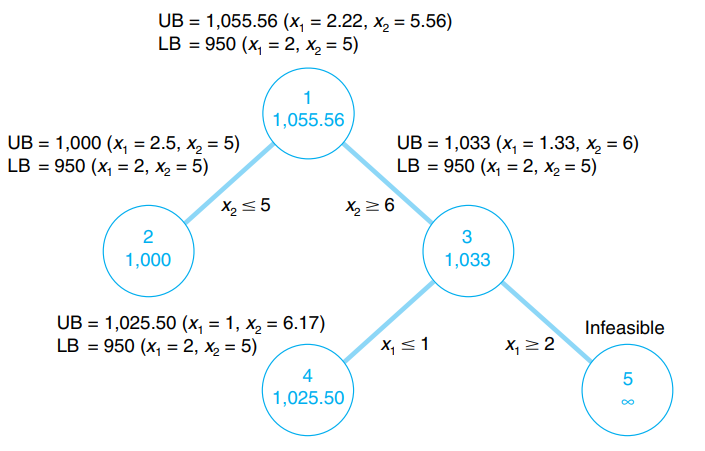
Todavía no tenemos una solución entera, por lo que tenemos que continuar con el algoritmo de bifurcación y límite.
Tercera conexión
El nodo 4 tiene la mejor UB. Dado que x_2 es la única variable que no es un número entero, nos bifurcaremos a esta variable.
Después de resolver los dos programas lineales en los nodos 6 y 7, obtenemos los siguientes resultados:
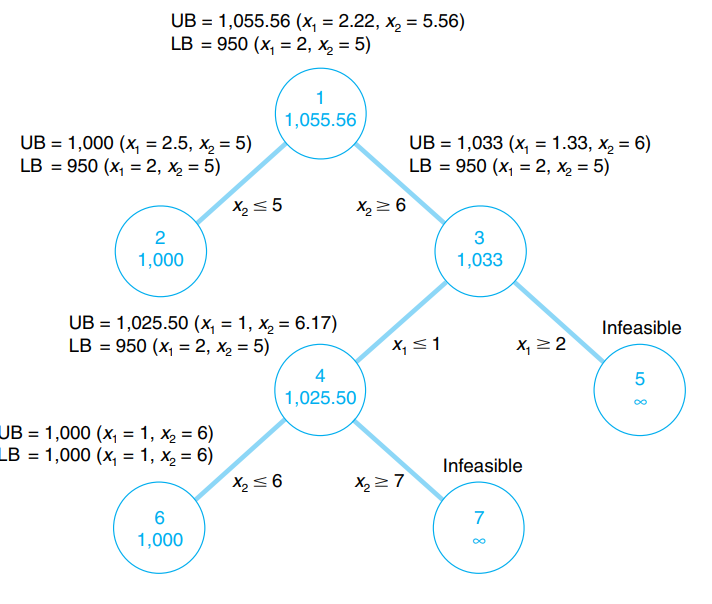
La solución al nodo 6 corresponde a los criterios del problema original (es decir, en número entero). Solo la rama en 3 y 4 tiene una UB superior al nodo 6, sin embargo, la rama que da a los nodos 5 y 7 no tiene solución factible. Concluimos que la solución óptima se encuentra en el nodo 6.
Resumen del método
Aquí hay un resumen en inglés del método que acabamos de usar.

