Dificultad
Fácil
25%
Proceso de Poisson
Un proceso de Poisson con parámetro λ es un proceso estocástico N (t) tal que N (O) = 0, N (t) se incrementa en +1 después de un tiempo T distribuido según una ley exponencial con parámetro λ. Hablamos de llegadas de Poisson si el tiempo entre dos llegadas es exponencial.
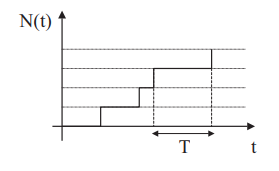
Tome como estado el valor de N(t), entonces el cadena de markov en tiempo continuo asociado al proceso de Poisson λ es:
Es posible conocer la probabilidad de que N sea el número k en el tiempo t mediante la fórmula:
N (t) se distribuye según una ley de Poisson con parámetro λt.
Los procesos de Poisson se asocian y descomponen de la siguiente manera:
- La superposición de n proceso de Poisson es un proceso de Poisson que tiene como parámetro la suma de los n parámetros
- Un proceso de Poisson que se descompone en n procesos con probabilidades pi. Estos n procesos son entonces procesos de Poisson con tasas respectivas λpI
ES 
FR 
EN