Contenido
PalancaAlgorítmico
Los algoritmos han existido desde siempre, es un proceso de pensamiento que se describe de manera lógica. Si bien este sistema nos parece hoy fundamental para muchas ciencias, la sistematización de la escritura algorítmica ha ido evolucionando a lo largo del tiempo y a través de la tecnología. Comenzó en la época de los babilonios, hasta que fue concretamente establecido por René Descartes en el método general propuesto por el Discurso sobre el método en 1637.

Los algoritmos modernos, incluido el llamado lenguaje de "programa", hicieron su debut poco después en 1677. El término que usamos hoy, "algoritmo", aparece dos siglos después.
El algoritmo de XXmi y XXImi century se basa a menudo en formalismos como el de las máquinas de Turing, que proporciona un marco científico para estudiar las propiedades de los algoritmos.
Con la informática, los algoritmos se desarrollaron mucho en la segunda mitad del XXmi Century y Knuth (1969), autor de The Art of Computer Programming definen 5 propiedades que constituyen los requisitos previos de un algoritmo.
1. Finitud: un algoritmo debe terminar después de un número finito de pasos.
2. Definición precisa: cada paso de un algoritmo debe definirse con precisión y sin ambigüedades.
3. Entradas: cantidades que se definen antes de que comience el algoritmo.
4. Productos: cantidades que tienen una relación específica con los insumos.
5. Rendimiento: todas las operaciones que debe realizar el algoritmo deben ser lo suficientemente básicas como para poder en principio ser realizadas en un periodo de tiempo finito por un hombre utilizando papel y lápiz.
Markov (1967) define un algoritmo como “una prescripción exacta que define un proceso de procesamiento que conduce desde los datos iniciales hasta el resultado final”.
Lo que implica las siguientes características:
• Precisión de la prescripción que no deja lugar a la arbitrariedad y la comprensión universal • Posibilidad de partir de datos iniciales que pueden variar dentro de límites dados • La orientación del algoritmo en la búsqueda de un resultado deseado que debe obtenerse al final de la ejecución de los datos iniciales: esta es la propiedad de conclusión del algoritmo.
Para Minsky (1967) la definición es aún más directa:
“Un conjunto de reglas que nos dicen, de momento en momento, exactamente cómo comportarnos”
Y finalmente para Stone (1972)
“Un algoritmo es un conjunto de reglas que define con precisión una secuencia de operaciones de modo que cada regla sea efectiva y esté definida y la secuencia se complete en un tiempo finito. »
Además especifica que:
“para quienes siguen las reglas del algoritmo, deben formularse de manera que se sigan mecánicamente sin tener que pensar”
Por ejemplo :
Si las instrucciones requieren extraer una raíz cuadrada y las realiza alguien que sabe hacer aritmética pero no sabe cómo extraer una raíz cuadrada, entonces se debe proporcionar un conjunto de reglas para extraer una raíz cuadrada, de modo que se cumpla la definición de el algoritmo
Se han desarrollado muchas herramientas formales o teóricas para describir algoritmos, estudiarlos, expresar sus cualidades y poder compararlos:
- estructuras algorítmicas: estructuras de control y estructuras de datos.
- las nociones de corrección, completitud y terminación.
- la teoria de complejidad.
Transcribir un algoritmo
LOSlenguaje natural : detallado y ambiguo, rara vez se usa para algoritmos complejos pero no está prohibido.
Pseudocódigo : un lenguaje estructurado, pero sin reglas estrictas definidas; Independiente de cualquier implementación
Organigrama : sin ambigüedad, buena legibilidad, escritura en forma de símbolos estandarizados
LOSlenguajes de programación : normalmente destinado a transcribir diagramas de flujo en una forma comprensible para las computadoras; También se puede utilizar para describir algoritmos.
LOSlenguajes algorítmicos : lenguaje que utiliza pseudocódigo compuesto de reglas fijas, comprensibles por una computadora, que permite la descripción y ejecución de algoritmos.
Estructura de control y estructura de datos
Una estructura de control es un comando que controla el orden en que se ejecutan las diversas instrucciones de un algoritmo o un programa de computadora. El procesador se encarga de memorizar la dirección de la siguiente instrucción a ejecutar, los bloques (bucles, if, etc.) o las subrutinas.
Esta secuencia de instrucciones también se denomina flujo de ejecución de un programa y se puede representar mediante un grafico de flujo de control o un autómata. Cierto paradigma de programación que llama a varios procesadores se expone entonces al problema de la asignación de tareas en los procesadores.
Una estructura de datos es una estructura lógica destinada a contener datos, con el fin de darles una organización que permita simplificar su procesamiento. Existen muchos tipos de estructura de datos en función de las acciones a realizar sobre ellos, no nos demoraremos más en este tema.
Cada lenguaje de computadora tiene un tipo de estructura de control y estructura de datos. La escritura de un algoritmo se basa muy a menudo en lenguajes ampliamente utilizados como C, java, etc.
Nociones de terminación, corrección, integridad
La terminación es la garantía de que el algoritmo terminará en un tiempo finito. Las pruebas de terminación generalmente involucran una función entera positiva estrictamente decreciente en cada paso / iteración del algoritmo.
Dada la garantía de que un algoritmo terminará, la prueba de corrección debe proporcionar la seguridad de que si el algoritmo termina dando una solución propuesta, entonces esta solución es correcta (en el sentido de que responde al problema planteado).
La prueba de integridad garantiza que, para un espacio de problema dado, el algoritmo, si termina, dará una solución para cada una de las entradas del algoritmo.
Terminación : el algoritmo tiene complejidad de tiempo.
Corrección : cualquier respuesta calculada del algoritmo es la solución del problema.
Lo completo : el algoritmo puede calcular una respuesta para cualquier instancia del problema.
Complejidad algorítmica
La complejidad de los algoritmos es una evaluación del costo de ejecutar un algoritmo en términos de tiempo (complejidad temporal) o espacio de memoria (complejidad espacial). Por tanto, la eficacia de un algoritmo depende de estos dos criterios, que intentaremos minimizar.
La complejidad algorítmica permite conocer la eficiencia intrínseca de un
algoritmo: el rendimiento "natural" de un algoritmo fuera del entorno en el que se implementará este último.
Existen varios tipos de análisis del rendimiento de un algoritmo:
- Análisis optimista (análisis del mejor de los casos o análisis del mejor de los casos).
- El análisis promedio es a menudo un factor en el paradigma de programación utilizado.
- Análisis pesimista (análisis del peor de los casos o análisis del peor de los casos).
Las clases de complejidad son conjuntos de problemas que tienen la misma complejidad según un determinado criterio. Las clases más conocidas son las clases definidas en máquinas de Turing (deterministas o no deterministas; consulte el curso sobre autómatas) con restricciones de tiempo y espacio. Existe una relación entre la complejidad algorítmica y su costo energético de operación, llamado principio de Landauer.
A continuación, se muestra una lista de las complejidades más comunes:
| Clasificación | Tipo de complejidad |
|---|---|
 | Complejidad constante: una tarea, un cálculo elemental, etc. |
 | complejidad logarítmica: dicotomía, árbol |
 | complejidad lineal: un bucle |
 | complejidad casi lineal: divide y vencerás, árbol |
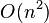 | Complejidad cuadrática: anidando dos bucles |
 | complejidad cúbica: anidamiento de tres bucles |
 | Complejidad polinomial: anidamiento de bucles sin conocimiento de estados. |
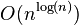 | Complejidad cuasi-polinomial: divide y vencerás |
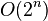 | complejidad exponencial: árbol, fuerza bruta |
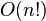 | Complejidad factorial: enfoque ingenuo de la enumeración combinatoria |
