Contenido
PalancaDesviaciones adicionales
Las desviaciones complementarias son utilizables si el primal es realizable y la solución está acotada, el dual es realizable y su solución también está acotada. Si los valores de las soluciones primal y dual son iguales, son óptimos para su programa lineal, hablamos de fuerte dualidad. A veces no es posible encontrar una solución, o no es útil calcularla. Estando vinculados el programa primario y el dual, es posible deducir una solución del programa recíproco utilizando las desviaciones complementarias.
Proceso
Uno de los principales teoremas de la teoría de la dualidad en programación lineal es el teorema de las desviaciones complementarias. Este teorema nos permite encontrar la solución óptima del problema dual cuando conocemos la solución óptima del problema primal (y viceversa) resolviendo un sistema de ecuaciones formado por las variables de decisión (primal y dual) y las restricciones (primal y dual). modelo doble).
La importancia de este teorema es que facilita la resolución de modelos de optimización lineal, permitiéndole encontrar el modelo más fácil de tratar (desde el punto de vista algorítmico). El proceso es el siguiente:
- Encuentre una solución viable en el primario.
- Si este es el caso, observe las variables distintas de cero (esto implica que la restricción del dual está saturada) y las restricciones con juego (lo que implica que la variable del dual es cero).
- Resuelve el sistema de ecuaciones
- Verifique la dualidad fuerte, es decir, la solución del primario es idéntica a la del dual. En este caso, la solución factible es óptima.
Versión I. Sean x * e y * las soluciones del primario y el dual. Estas dos soluciones son óptimas si y solo si:
- para cualquier j de 1 an
- o la restricción j del dual está saturada
- o x *j=0
- o ambos
- para todo i de 1 am
- o la restricción i del primario está saturada
- o y *I=0
- o ambos
La segunda versión de las desviaciones complementarias permite comprender mejor cómo encontrar una solución en el programa recíproco. Para ello se debe asumir que las dos condiciones de la versión I son siempre verdaderas.
Versión II. Una solución x del primal es óptima si y solo si existe un vector y * tal que:
- y * es elegible
- si xj> 0 entonces la j-ésima restricción del dual está saturada
- si la restricción i-ésima del primario no está saturada, entonces y *I=0.
- ya la inversa entre lo dual y lo primario.
Así, una vez que se encuentra una solución en el programa recíproco, solo queda verificar la fuerte dualidad del sistema.
Ejemplo 1
Considere el siguiente modelo de programación lineal con 2 variables cuya solución óptima es X = 14/5 e Y = 8/5 con el valor óptimo V = 20,8.

El modelo dual asociado con el modelo primario es:

Entonces, el teorema de las desviaciones complementarias muestra las siguientes relaciones:

Como sabemos, X = 14/5 e Y = 8/5 (solución óptima primaria). Si reemplazamos estos valores de X e Y en la tercera y cuarta ecuaciones (porque ambas restricciones del primario están saturadas y no podemos concluir nada sobre las ecuaciones 1 y 2), generamos un sistema de ecuaciones en términos de A y de B cuya solución corresponde a A = 6/5 y B = 2/5. Si luego evaluamos la función objetivo en el problema dual de esta solución, obtenemos: V = 12 (6/5) +16 (2/5) = 20.8, que es similar al valor óptimo del problema primario (dualidad fuerte ).
Ejemplo 2
Considere el siguiente problema:
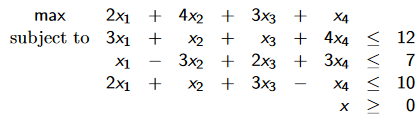
La solución a este problema es {42, 0, 10.4, 0, 0.4}. El problema dual es el siguiente:
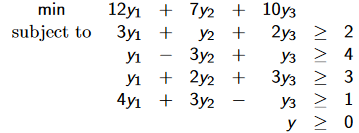
Prueba de viabilidad. La primera restricción está saturada, no hay conclusión para y1. La segunda restricción no está saturada, entonces y2 = 0. La tercera restricción está saturada, nada en y3.
Variables positivas. x1 = 0, nada para concluir. x2> 0, la segunda restricción del dual está saturada. x3 = 0, nada para concluir. x4> 0, la cuarta restricción del dual está saturada.
Entonces, la solución de dual debe satisfacer: y2 = 0; y1 + y3 = 4; 4y1 + y3 = 1 con {1, 0, 3} como solución. Los valores de primal y dual son equivalentes, por lo que tenemos el óptimo.
