Contenido
PalancaPrueba de Dickey-Fuller
La prueba de Dickey-Fuller es una forma de determinar si el proceso (serie de tiempo) tiene una raíz unitaria.

Bases
Consideramos el proceso estocástico de la forma.
![]()
donde |φ| ≤ 1 y εi es ruido blanco. Si |φ| = 1, tenemos lo que llamamos raíz unitaria. En particular, si φ = 1, tenemos un paseo aleatorio (sin deriva), que no es estacionario. De hecho, si |φ| = 1, el proceso no es estacionario, mientras que si |φ| < 1, el proceso es estacionario. No consideraremos el caso donde |φ| > 1 más ya que en este caso se dice que el proceso es explosivo y aumenta con el tiempo.
Este proceso es un proceso autorregresivo de primer orden, AR(1), que estudiamos con más detalle en Procesos autorregresivos. También veremos por qué estos procesos sin raíz unitaria son estacionarios y por qué se utiliza el término "raíz".
La prueba de Dickey-Fuller es una forma de determinar si el proceso anterior tiene una raíz unitaria. El enfoque utilizado es bastante simple. Primero calcule la primera diferencia, es decir
![]()
es decir
Si usamos el operador delta, definido por Δyi = yi – yi-1 y definimos β = φ – 1, entonces la ecuación se convierte en la ecuación de regresión lineal
![]()
donde β ≤ 0 y por lo tanto la prueba para φ se transforma en una prueba según la cual el parámetro de pendiente β = 0. Por lo tanto, tenemos una prueba unilateral (ya que β no puede ser positiva) donde
H0: β = 0 (equivalente a φ = 1)
H1: β < 0 (equivalente a φ < 1)
Bajo la hipótesis alternativa, si b es la estimación de mínimos cuadrados ordinarios (MCO) de β y, por lo tanto, φ-bar = 1 + b es la estimación de mínimos cuadrados ordinarios (MCO) de φ, entonces, para n suficientemente grande
![]()
o
Podemos utilizar el método habitual de regresión lineal, excepto que cuando la hipótesis nula es verdadera, el coeficiente t no sigue una distribución normal y, por tanto, no podemos utilizar la prueba t habitual. En cambio, este coeficiente sigue una distribución tau, por lo que nuestra prueba es si el estadístico tau τ (que es equivalente al estadístico t habitual) es menor que τcrit según una tabla de valores críticos del estadístico tau que se muestra en la tabla de Dickey-Fuller. .
Si el valor tau calculado es menor que el valor crítico en la tabla de valores críticos, entonces tenemos un resultado significativo; en caso contrario, aceptamos la hipótesis nula de que existe una raíz unitaria y que la serie temporal no es estacionaria.
Existen las siguientes tres versiones de la prueba de Dickey-Fuller:
Tipo 0 Sin constante, sin tendencia Δyi = β1 yi-1 + εi
Tipo 1 Constante, sin tendencia Δyi = β0 + β1 yi-1 + εi
Tipo 2 Constante y tendencia Δyi = β0 + β1 yi-1 + β2 i+ εi
Cada versión de la prueba utiliza un conjunto diferente de valores críticos, como se muestra en la tabla de Dickey-Fuller. Es importante seleccionar la versión correcta de la prueba para la serie temporal que se analiza. Tenga en cuenta que la prueba de tipo 2 supone que existe un término constante (que puede ser significativamente igual a cero).
Ejemplo
Las ganancias netas diarias de un jugador pequeño se enumeran en la columna B de la Figura 1. Utilice la prueba de Dickey-Fuller para determinar si la serie de tiempo es estacionaria.
Empezamos asumiendo que el modelo correcto es el tipo 1, es decir, constante pero sin tendencia.
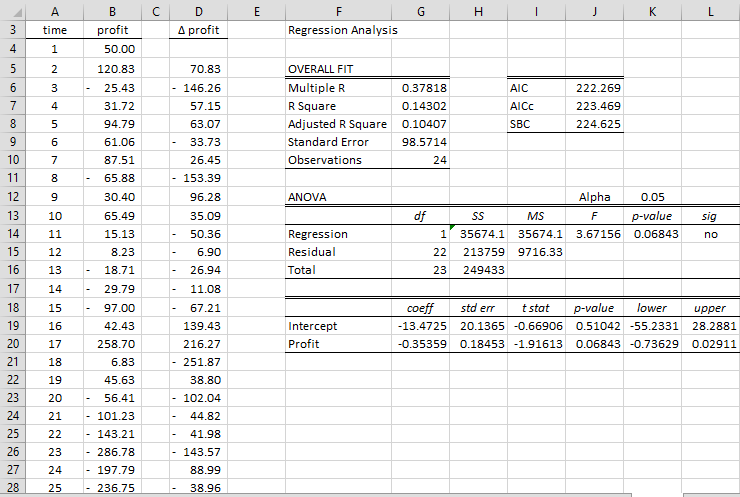
Dado que utilizamos el modelo de regresión
(constante, sin tendencia), utilizamos la herramientaanálisis de datos Regresión lineal de Real Statistics usando el rango B4:B27 y el rango de datos, resaltando el rango D5:D28 y presionando Ctrl-D.
El resultado del análisis de regresión se muestra en el lado derecho de la figura. En particular, vemos que el estadístico t (celda I20) para el coeficiente β1 es -1,91613. Esta es la estadística tau. Ahora miramos la tabla de Dickey-Fuller y vemos que el valor crítico de tau para una prueba de Tipo 1 es -2,986 cuando n = 25 y α = 0,05. Dado que τcrit = -2,986 < – 1,91613 = τ, no podemos rechazar la hipótesis nula de que la serie temporal no es estacionaria.
Tenga en cuenta que el coeficiente β1 (celda G20) es negativo como se esperaba. Si por el contrario el coeficiente fuera positivo, entonces sabríamos que este tipo de prueba de Dickey-Fuller es inapropiada ya que β1 = φ – 1 ≤ 0.
Ahora mostramos en la figura un gráfico de los valores de la serie temporal de la figura anterior.
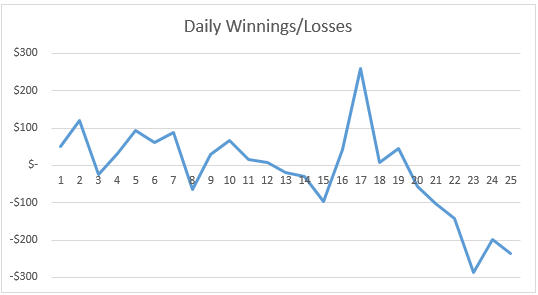
Vemos una aparente tendencia a la baja hacia el final del período de 25 días, por lo que no sorprende que la serie temporal no sea estacionaria. De hecho, esto nos lleva a elegir el test de Dickey-Fuller tipo 2 (con constante y tendencia). El resultado de esta prueba se muestra en la figura.
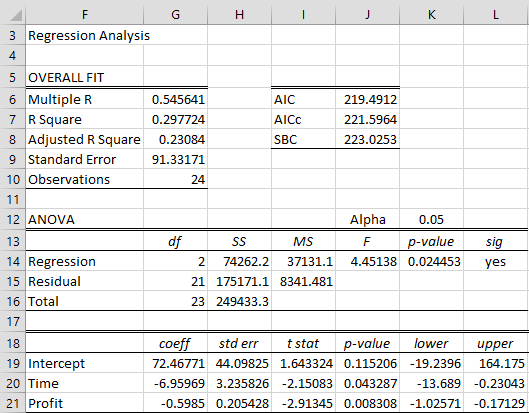
Dado que utilizamos el modelo de regresión
Δyi = β0 + β1i + β2yi-1 + εi
esta vez usamos A4:B27 de la Figura 1 como el rango de datos X y D5:D28 como el rango de datos Y. Vemos en la Figura 3 que el estadístico t (celda I21) para el coeficiente β2 es -2, 91345. Ahora miramos la tabla de Dickey-Fuller y vemos que el valor crítico de tau es -3,60269 para una prueba de Tipo 2 cuando n = 25 y α = 0,05. Dado que τcrit = -3,60269 < -2,91345 = τ, no podemos rechazar la hipótesis nula de que la serie temporal no es estacionaria.
